СРОЧНО!!

Докажите, что треугольник с вершинами А (4; 2), В (0; -6), С (-4; -2) является
равнобедренным.

Ответы

Ответ дал: Artem112

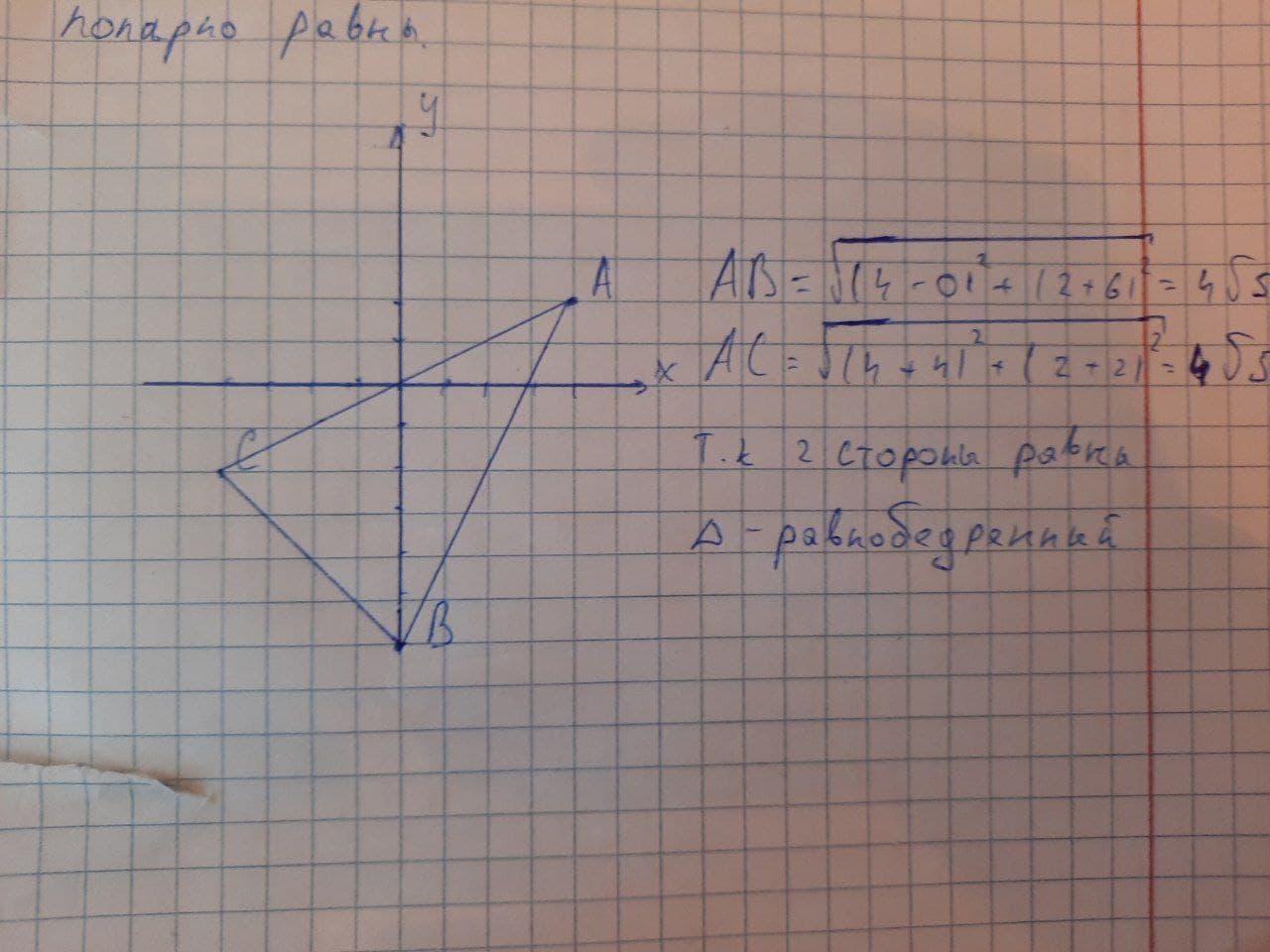
Найдем длины сторон:

$AB=\sqrt{(0-4)^2+(-6-2)^2} =\sqrt{16+64} =\sqrt{80}$

$BC=\sqrt{(-4-0)^2+(-2-(-6))^2} =\sqrt{16+16}=\sqrt{32}$

$AC=\sqrt{(-4-4)^2+(-2-2)^2} =\sqrt{64+16}=\sqrt{80}$

Так как $AB=AC$ , то треугольник равнобедренный.

Аноним: большого любителя жесткого секса
одетого в куртку в ботинки обутого
Ева Нутова Еба Нутого

Аноним: ааааааа

Ответ дал: lochgipon

Ответ:

Решение во вложении:

Объяснение:

т.к две стороны равны 4√5 треугольник равнобедренный

Приложения:

Аноним: да уж...

Аноним: ептаъ

Аноним: да не еби мозги

Похожие вопросы

Русский язык

1 год назад

Русский язык

1 год назад

Русский язык

2 года назад

Русский язык

2 года назад

Математика

7 лет назад

Математика

7 лет назад

Геометрия

9 лет назад

Математика

9 лет назад