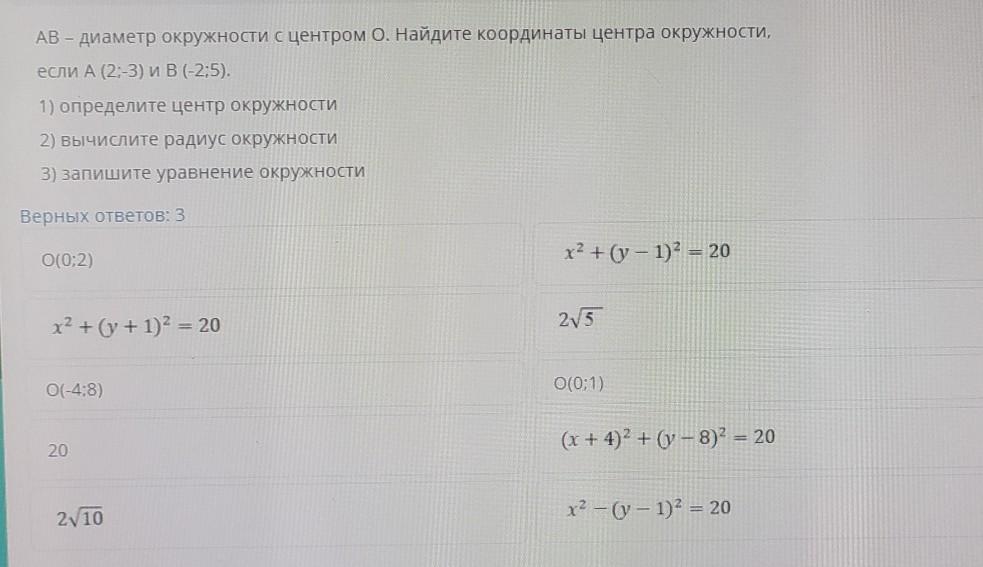
AB - диаметр окружности с центром О. Найдите координаты центра окружности,
если А (2;-3) и B(-25).
1) определите центрокружности
2) вычислите радиус окружности
3) запишите уравнение окружности​

Ответ:

1) О(0;1).

2) R = 2√5 ед.

3)  x² + (y-1)² = 20.

Объяснение:

1) центр окружности - середина отрезка АВ.

Координаты середины отрезка - полусумма соответствующих координат начала и конца отрезка, то есть:

Хо = (2+(-2))/2 = 0.  Yo(-3+5)/2 = 1.  Итак, центр окружности:

О(0;1).

2) Радиус окружности  - модуль отрезка АО.

|AO| = √((Xo-Xa)² + (Yo-Ya)²) = √((0-2)² + (1-(-3))²) = √20 = 2√5.

R = 2√5 ед.

3) уравнение окружности в общем виде:

(x - Xo)² + (y - Yo)² = R². В нашем случае:

x² + (y-1)² = 20.