На відстані
5см від центра кулі проведено переріз, площа якого дорівнює
144п см2. Знайдіть об’єм кулі

Ответ: объём шара равен см³

Пошаговое объяснение:

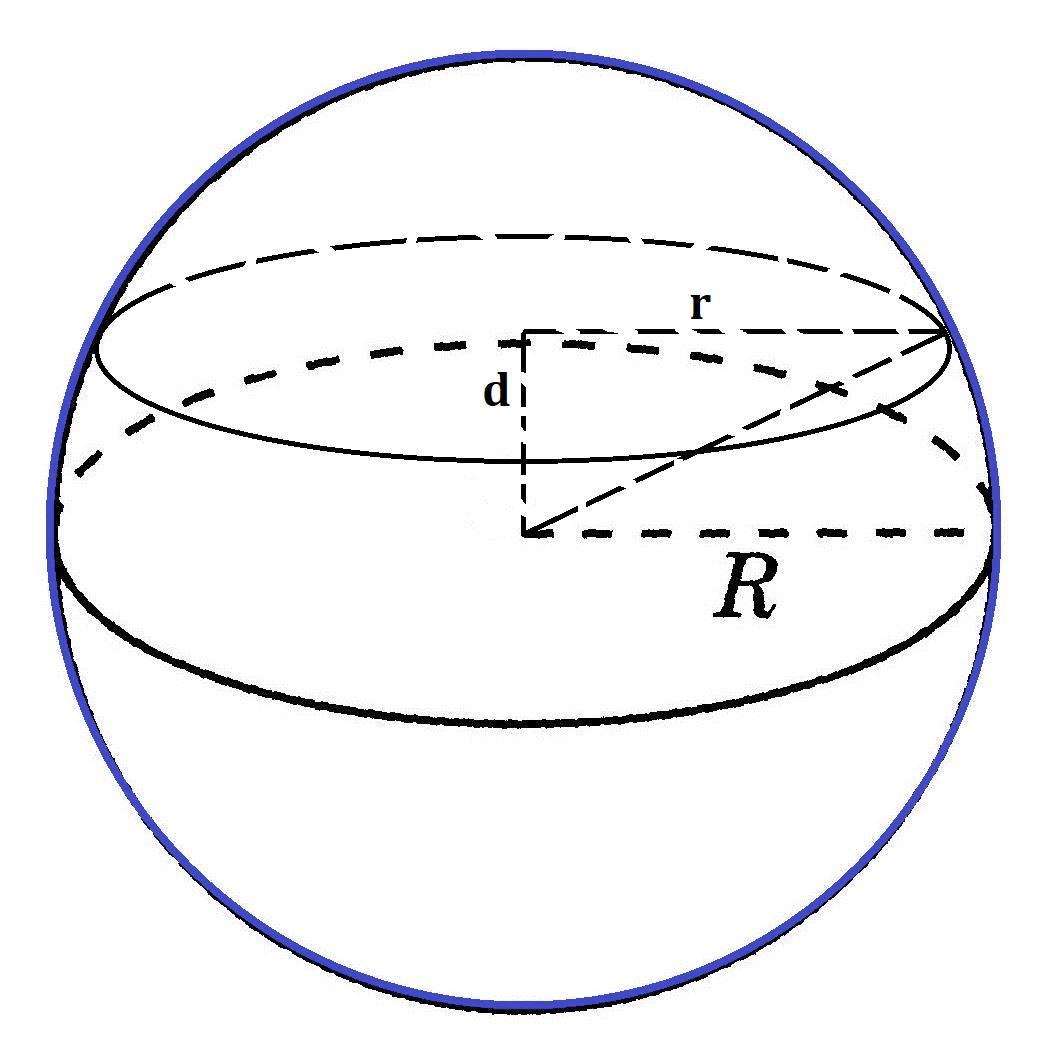
d = 5 см - расстояние от центра шара но сечения

R - радиус шара

r - радиус сечения, находящееся на расстоянии 5 см от центра шара

Сечение, находящееся на расстоянии 5 см от центры шара - круг.

• Площадь круга равна произведению числа пи на квадрат его радиуса.

S сечения = π · r² = 144π см²

⇒ r = √(S сечения/π) = √(144π/π) = √144 = 12 см

Видим прямоугольный треугольник, где d и r - его катеты, а R - его гипотенуза

Найдём R по теореме Пифагора:

см

• - объём шара

см³