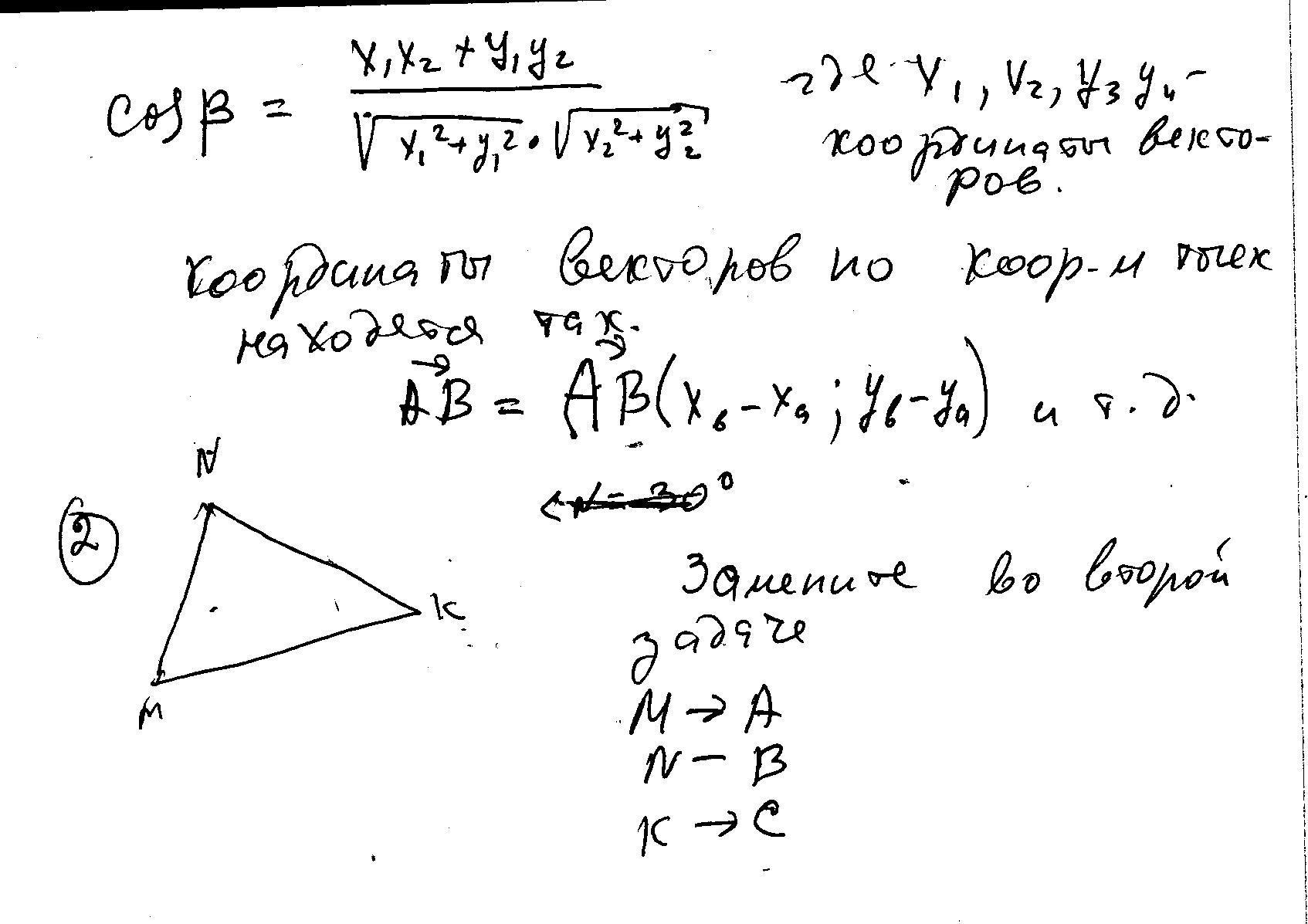
1) Найдите косинусы углов треугольника ABC, если A (1;7) B(-2;4) C(2;0)

2)Решите треугольник MNK, если угол n=30, k=105 nk=3 корня из 2

Помогите с решением пожайлуста

Ответы

Ответ дал: ужнеужели

Во второй задаче выкладываю ранее решенное. Просто замените букочки в обозначении треугольника на нужные Вам.

Приложения:

Ответ дал: xERISx

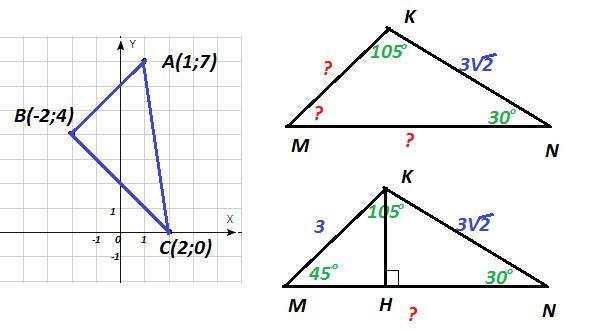
1) Дано : ΔABC; A (1;7); B(-2;4); C(2;0)

Найти : cos A, cos B, cos C

Решение :

$AB=sqrt{big(x_B-x_Abig)^2+big(y_B-y_Abig)^2}=\\~~~~~=sqrt{big(-2-1big)^2+big(4-7big)^2}=sqrt{18}=3sqrt2\\AC=sqrt{big(x_C-x_Abig)^2+big(y_C-y_Abig)^2}=\\~~~~~=sqrt{big(2-1big)^2+big(0-7big)^2}=sqrt{50}=5sqrt2\\CB=sqrt{big(x_B-x_Cbig)^2+big(y_B-y_Cbig)^2}=\\~~~~~=sqrt{big(-2-2big)^2+big(4-0big)^2}=sqrt{32}=4sqrt2$

По теореме косинусов

a² = c² + b² - 2cb·cos α

$cosalpha =dfrac{c^2+b^2-a^2}{2cb}\\\cos A =dfrac{AB^2+AC^2-CB^2}{2cdot ABcdot AC}=dfrac{sqrt{18}^2+sqrt{50}^2-sqrt{32}^2}{2cdot 3sqrt2cdot 5sqrt2}=\\~~~~~~~=dfrac{18+50-32}{2cdot 3cdot 5cdot2}=dfrac{36}{60}=dfrac 35\\\cos B =dfrac{AB^2+CB^2-AC^2}{2cdot ABcdot CB}=dfrac{sqrt{18}^2+sqrt{32}^2-sqrt{50}^2}{2cdot 3sqrt2cdot 4sqrt2}=\\~~~~~~~=dfrac{18+32-50}{2cdot 3cdot 4cdot2}=dfrac{0}{48}=0$

$cos C =dfrac{AC^2+CB^2-AB^2}{2cdot ACcdot CB}=dfrac{sqrt{50}^2+sqrt{32}^2-sqrt{18}^2}{2cdot 5sqrt2cdot 4sqrt2}=\\~~~~~~~=dfrac{50+32-18}{2cdot 5cdot 4cdot2}=dfrac{64}{80}=dfrac45$

Ответ : $boldsymbol{cos A=dfrac 35;~cos C =dfrac 45;~cos B=0,~~Rightarrow~angle B=90textdegree}$

============================================

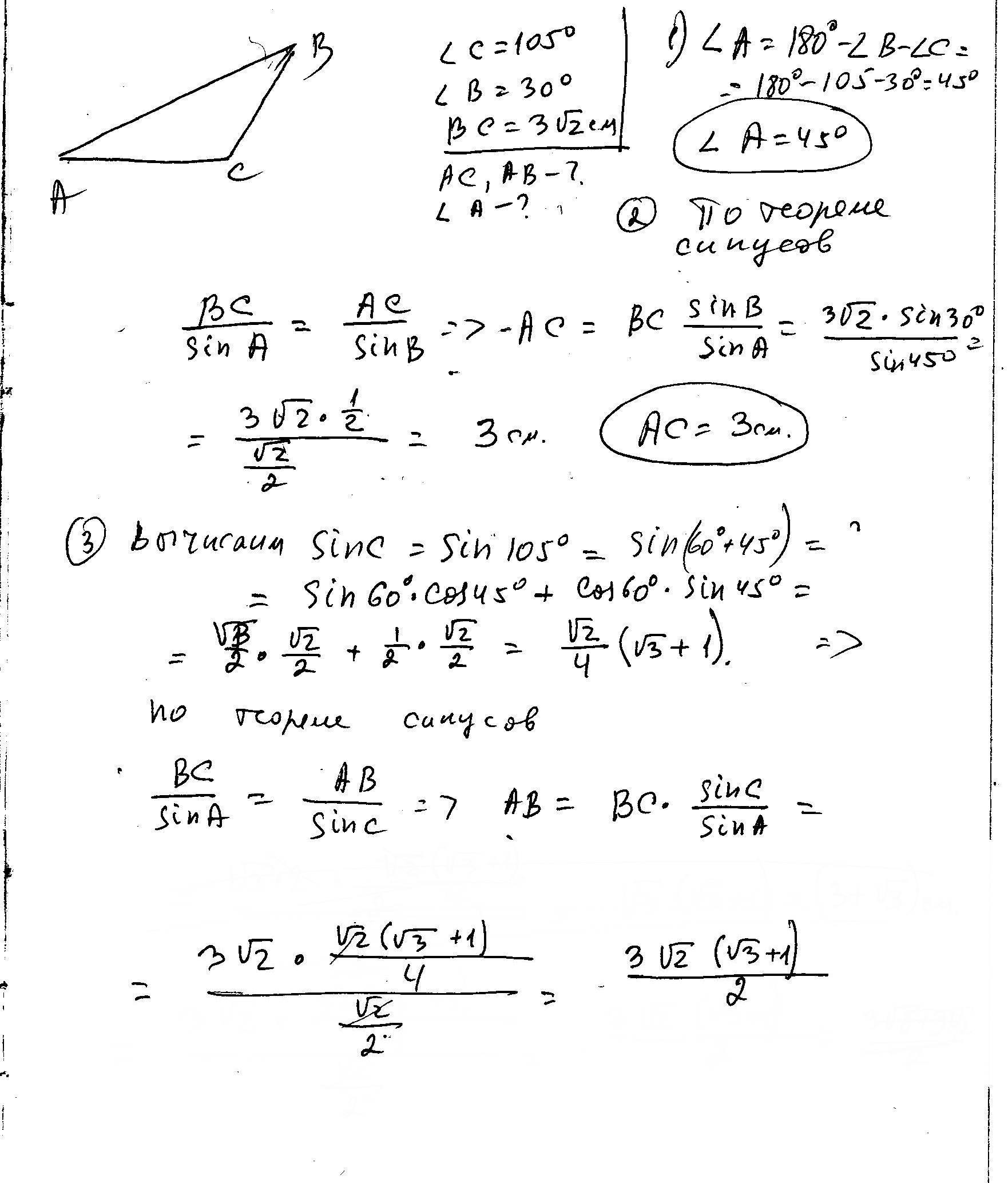
Дано : ΔMNK; ∠N=30°; ∠K=105°; NK=3√2

Найти : ∠M, MN, MK, $S_{Delta MNK}$

Решение : сумма углов треугольника равна 180° ⇒

∠M = 180° - (∠N + ∠K) = 180° - (30° + 105°) = 45°

По теореме синусов

$dfrac{NK}{sin M}=dfrac{MK}{sin N}~~~Rightarrow~~MK=dfrac{NKcdot sin N}{sin M}\\MK=dfrac{3sqrt2cdot sin 30textdegree}{sin 45textdegree}=dfrac{3sqrt2cdot frac 12}{frac{sqrt2}2}=3sqrt2cdot dfrac 12cdot dfrac2{sqrt2}=3$