ПОМОГИТЕ ДАЮ 100 БАЛЛОВ)
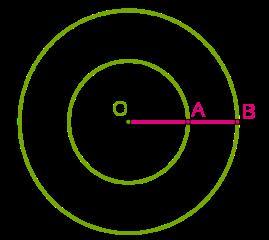
Даны два круга с общим центром O.
Площадь меньшего круга равна 147см2. Отрезок AB = 4 см.
Значение числа π≈3.

Определи площадь большего круга.

S =
см².

Решение и ответ:

Sм = 147 см² - площадь меньшего круга

AB = 4 см - отрезок

π ≈ 3

Для определения площади большего круга нужно найти его радиус OB.

OB = AB + OA

1. Найдем радиус меньшего круга OA.

Площадь меньшего круга равна:

Sм = πr², где r - радиус = OA

OA = √(Sπ)

OA = √(147 · 3)

OA = √441

OA = 21 см

2. Площадь большего круга равна:

S = πR², где R - радиус = OB

OB = AB + OA

Определим радиус большего круга:

OB = AB + OA

OB = 4 + 21 = 25 см

S = 3 · 25² = 3 · 625 = 1875 см²

Ответ: 1875 см².