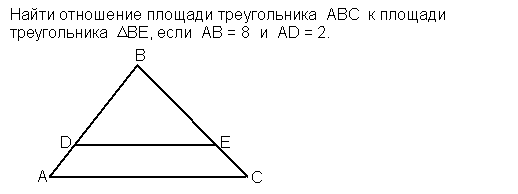
Найдите отношение площади треугольника ABC к площади треугольника DBE, если AB=8 и AD=2
Приложения:
Ответы
Ответ дал:
0
Условие неполное. Вероятно, подразумевается, что DE║AC.
Если это так, то
∠BDE = ∠BAC как соответственные при пересечении параллельных прямых DE и AC секущей ВА, угол В общий для треугольников АВС и DBE, значит треугольники подобны по двум углам.
Коэффициент подобия:
k = AB : DB = 8 : (8 - 2) = 4 : 3
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Sabc : Sdbe = k² = 16 : 9
Если это так, то
∠BDE = ∠BAC как соответственные при пересечении параллельных прямых DE и AC секущей ВА, угол В общий для треугольников АВС и DBE, значит треугольники подобны по двум углам.
Коэффициент подобия:
k = AB : DB = 8 : (8 - 2) = 4 : 3
Площади подобных треугольников относятся как квадрат коэффициента подобия:
Sabc : Sdbe = k² = 16 : 9
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
10 лет назад
10 лет назад
10 лет назад