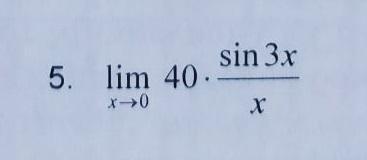Предмет: Математика
Автор: amestrisq
Вопрос задан 7 лет назад

< >

(5)ВЫчислите предел функции

Приложения:

Ответы

Ответ дал: zveryakovanata

1

Ответ: 120

Пошаговое объяснение: =|0/0|= lim 40· 3·(Sin3x/3x)= 120·1=120 Применили 1-й замечательный предел lim (Sin3x)/3x=1 при х→0

Ответ дал: NNNLLL54

1

Ответ:

$\lim\limits _{x \to 0}\, 40\cdot \dfrac{sin3x}{x}=\Big[\ \dfrac{0}{0}\ \Big]=40\cdot \lim\limits _{x \to 0}\Big(\underbrace{\dfrac{sin3x}{3x}}_{1}\cdot 3\Big)=40\cdot \lim\limits _{x \to 0}\ (1\cdot 3)=40\cdot 3=120\\\\\\\\P.S.\ \ \ \lim\limits _{\alpha (x) \to 0}\dfrac{sin\alpha (x)}{\alpha (x)}=1\ \ \ \ \ ,\ \ \alpha (x)=3x\ .$

Похожие вопросы

Английский язык

1 год назад

Помогите пожалуйста очень срочно!!! C. Choose the right option. 21. I bought a …….. green bag. a. French b. leather c. smart 22. It’s the ………. film I have ever seen. a. funny b. funnier c.

Английский язык

1 год назад

МНЕ СРОЧНО! ДАМ 30 БАЛЛОВ! Все отмеченые задания)

Математика

2 года назад

143 $143 \div \frac{1}{4 } + \frac{1}7}$

Алгебра

2 года назад

поточках накреслити малюнок

Математика

8 лет назад

Разрежте квадрат на 4 равных пятиугольника. Помогите :(

Алгебра

8 лет назад

0,5y^3-0,5y(y+1)(y-3)=7

Математика

9 лет назад

длина зеркала прямоугольной формы 6 см , а ширина третья часть длины .Чему равна площадь 6 таких зеркал?

Алгебра

9 лет назад

Вычислите, используя свойства степени с натуральным показателем: