Найти производную функции:
y = х^2 +5/4х-1
Аноним:
Если у=х^2 + 5/(4x-1), то y'=2x - 5*(4x-1)^(-2) * 4=2x - 20/(4x-1)^2
Надо ставить скобки на экране. Практически уверена, что Вы подразумевали это условие))
Хотя может быть и y=x^2 + (5/4)*x - 1; y=x^2 + 5/(4x) - 1
И даже у=x^2 + 5/(4*x^(-1)) В условии часто х5 + х-2 означает х^5 + x^(-2)
Ответы
Ответ дал:
0
решение производной вкидываю на фото
Приложения:
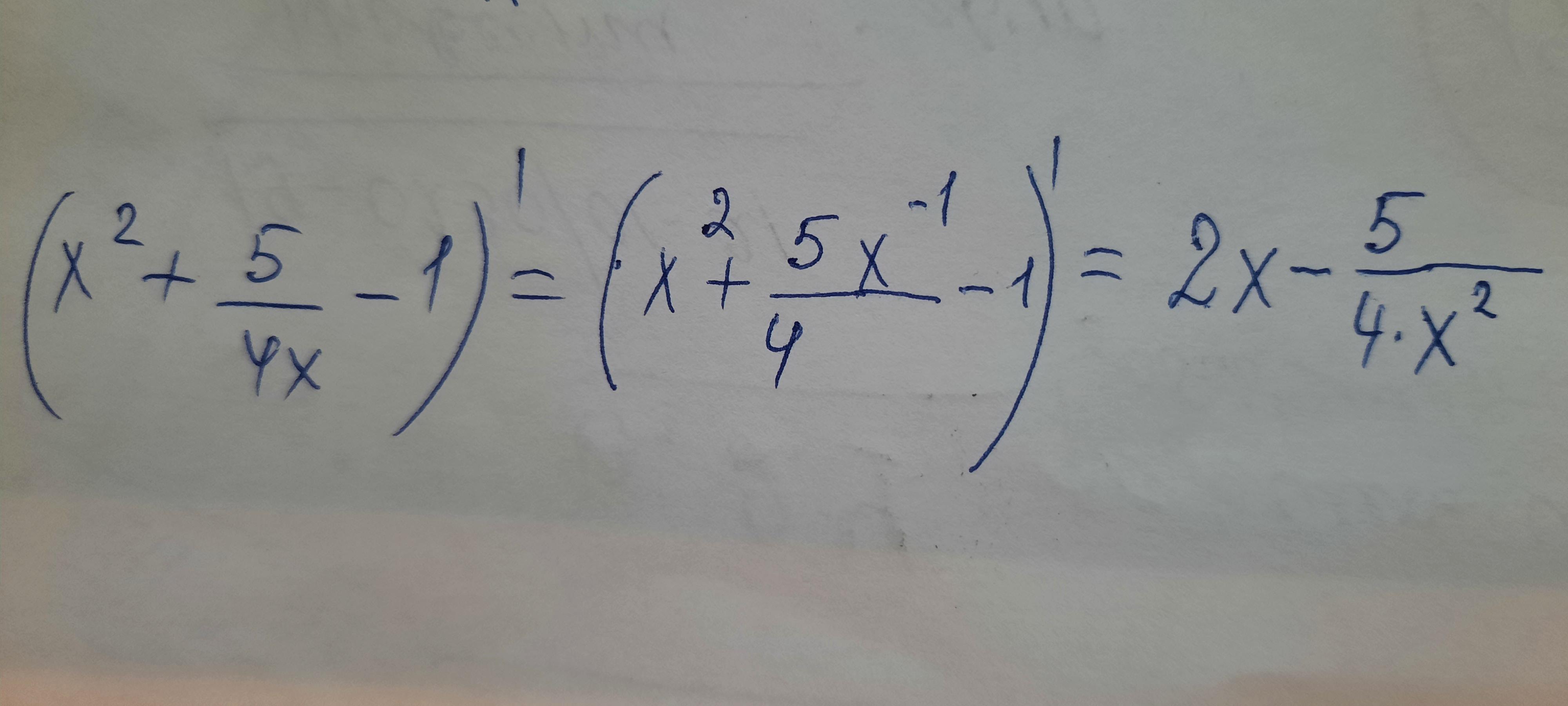
Ответ дал:
1
Ответ:
Пошаговое объяснение:
Похожие вопросы
1 год назад
2 года назад
8 лет назад
9 лет назад