Перпендикуляр проведений з вершини прямокутника до його діагоналі, ділить кут який відноситься як 4:5. Знайдіть кут між перпендикуляром та іншою діагоналлю

Ответ:

угол между перпендикуляром и другой диагональю =10°

Объяснение:

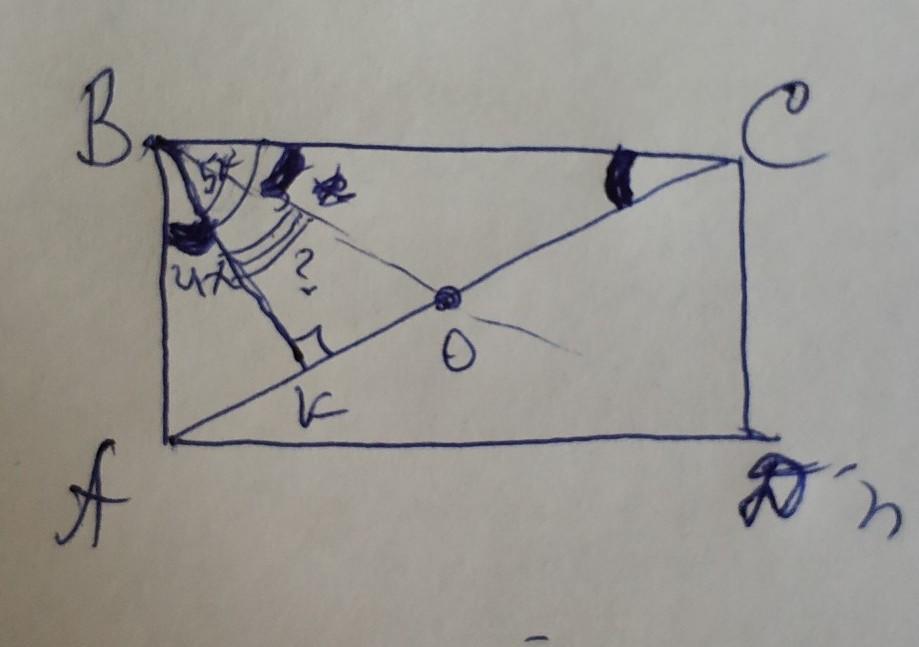
прямоугольник ABCD: BK_|_AC

<ABK:<CBK=4:5

пусть х (х>0) - коэффициент пропорциональности, тогда <ABK=4x, <CBK=5x

<B=<ABK+<CBK, <B=90°

4x+5x=90°

x=10°

<ABK=40°, <CBK=50°

∆BKC: <BCK=40°

∆BOC:<CBO=<BCO=40°

<KBC=<KBO+<OBC

90°=<KBO+40°

<KBO=10°