в 2 концентрических окружностях радиусы которого равны 25 см и 17 см требуется провести хорду чтобы часть её, лежащего во внутренней окружности составляла 2/5 всей хорды. Определите длину хорды.​

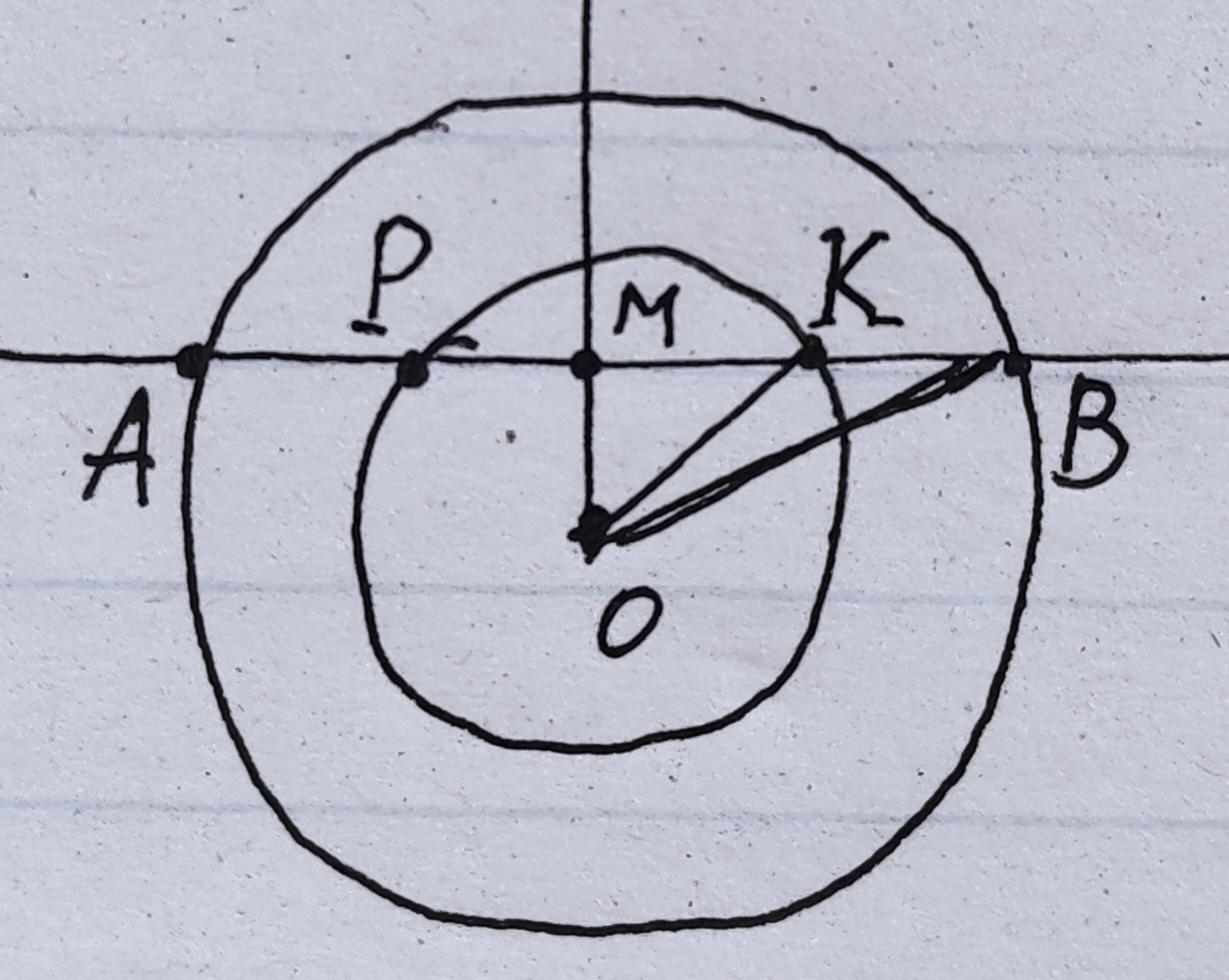
Пусть хорда АВ= Х см пересекает малую окружность в точках Р и К. Пусть ОМ перпендикулярно АВ.

По условию РК= 2/5*х => МК=1/5*х =0,2х, тк радиус перпендикулярный хорде делит её пополам.

КВ=АР=(х-2/5*х) : 2=3/10*х=0,3х.

Тогда МВ=0,5х. По условию ОК=17 см, ОВ=25 см.

Выразим их прямоугольных треугольников ∆ ОМК, ∆ОМВ катет ОМ ( по т Пифагора)и составим уравнение

√(17²-0,04 х²) =√(25²-0,25х²),

289-0,04 х²=625²-0,25 х²,

0,21х²=336=> Х=40.

АВ=40 см.