Я что-то не вырубаюсь где я допустил ошибку ?
Приложения:
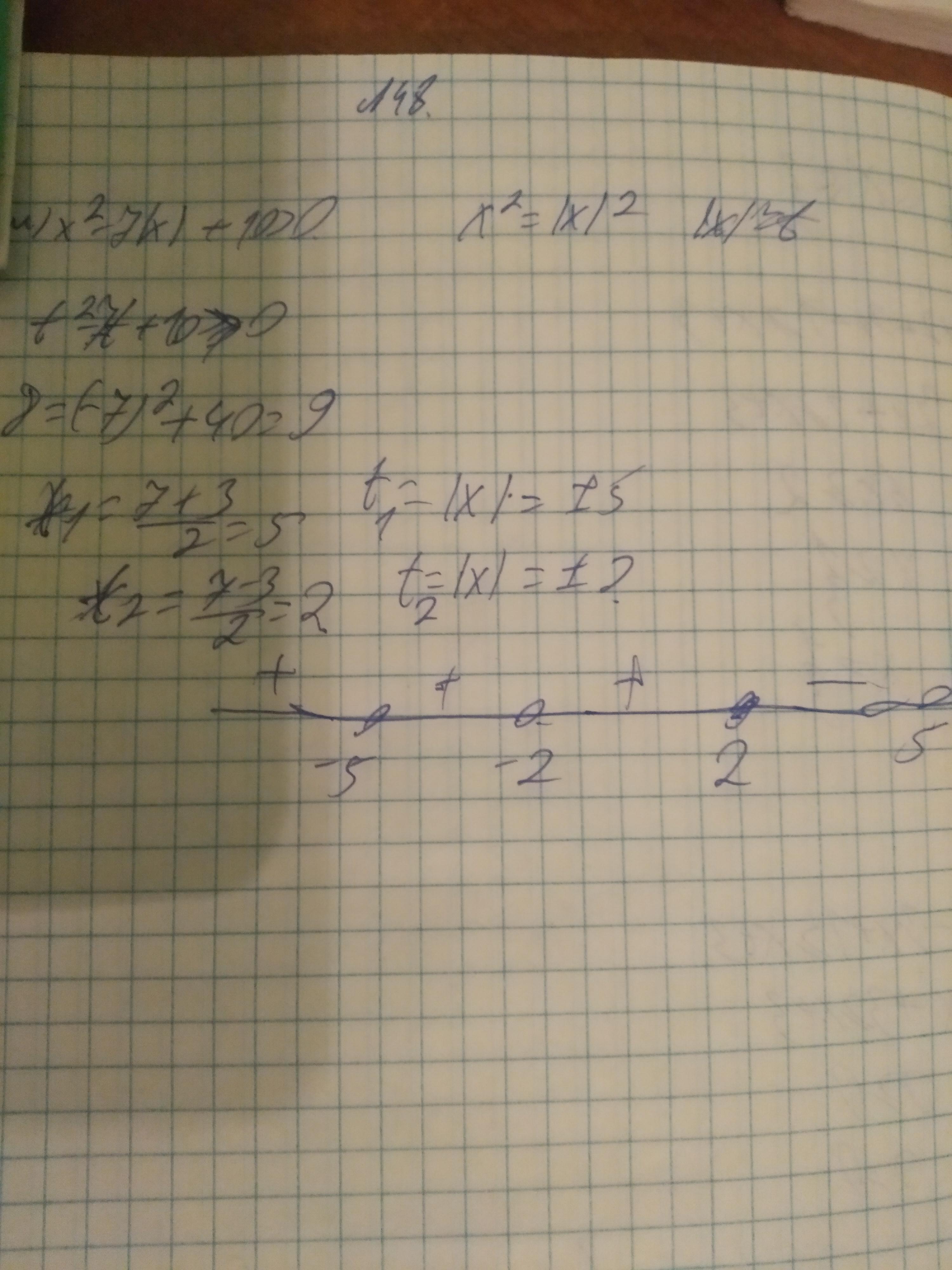
Reqiuem10:
Просто ответ - бес до -5 (-2;2)(5;+ бес
Но я на -5;-2 тоже получаю +
А ладно я понял , я должен было в х²-7|х| +10>0 поставить цифры а не в т²-7т+10>0
Ответы
Ответ дал:
0
Ответ:
Извините, решение не открывалось.
Ответ дал:
0
Ответ:
(см. объяснение)
Объяснение:
Задание выполнено!
Похожие вопросы
2 года назад
2 года назад
2 года назад
8 лет назад
9 лет назад
9 лет назад