Задан рисунок:

1.png

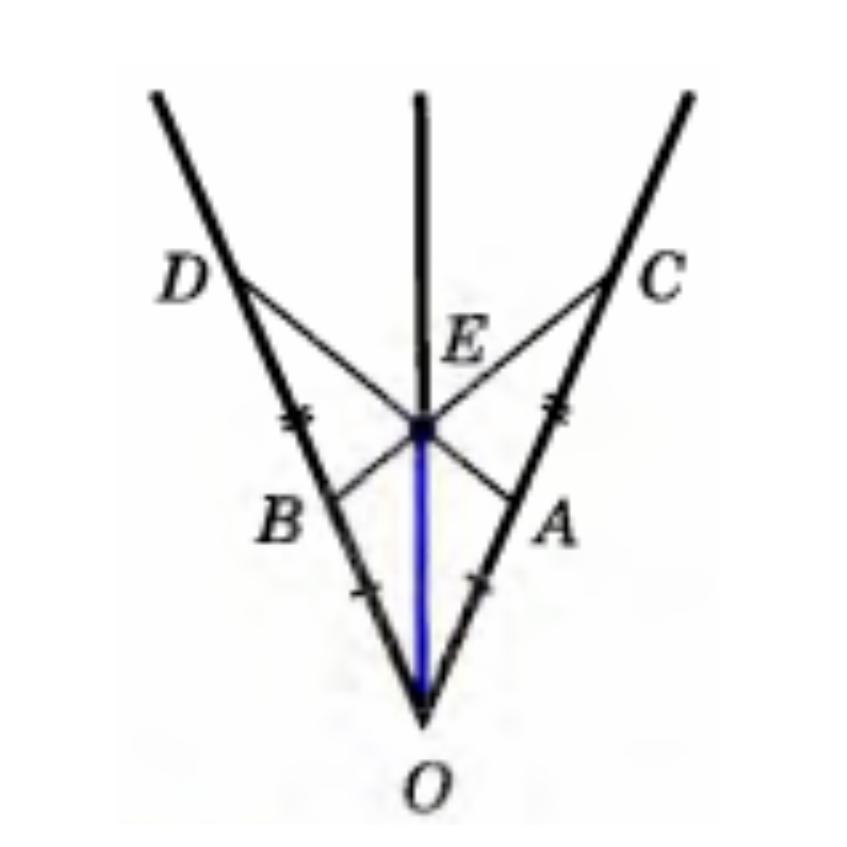
На рисунке: OA = OB; BD = AC. Точка E – точка пересечения прямых AD и BC. Докажите, что OE – биссектриса угла DOC.

Указание: для решения задачи необходимо воспользоваться тремя различными признаками равенства для различных пар треугольников.

siestarjoki: луч OE делит угол DOC, конечно

cos20093: △BDE=△ACE уже достаточно, потому что E равноудалена от сторон угла DOC. Равенство треугольников означает, что существует движение, при котором они совпадают => совпадают и соответствующие высоты (иначе можно было бы два перпендикуляра провести к одной прямой через одну точку). Так что можно обойтись 2 парами треугольников :)