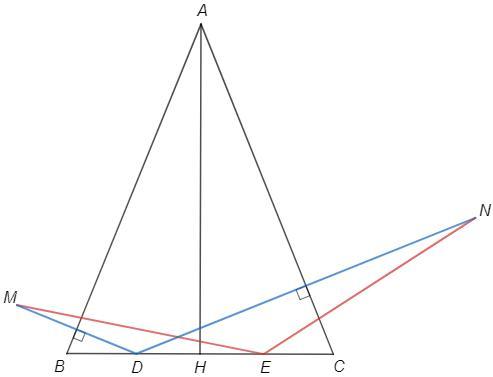
На основании BC равнобедренного треугольника ABC выбрана точка D. Точки M и N симметричны D относительно прямых AB и AC соответственно, точка E симметрична D относительно биссектрисы угла A. Найдите угол MEN, если ∠ABC=68∘.
Ответы
Ответ дал:
1
Симметрия относительно прямой:
AB - серединный перпендикуляр к DM, AD=AM
AH - серединный перпендикуляр к DE, AD=AE
AC - серединный перпендикуляр к DN, AD=AN
Точки M D E N равноудалены от точки A и лежат на одной окружности.
∠MEN=∠MDN (вписанные, опираются на MN)
B=C=68 (△ABC - р/б)
MDB=90-B, NDC=90-C
MDN =180-MDB-NDC =B+C =2*68 =136° =MEN
Приложения:
Похожие вопросы
2 года назад
2 года назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
9 лет назад