СРОЧНО‼️
У трикутнику центр ОПИСАНОГО кола лежить на висоті. Доведіть що цей трикутник рівнобедренний
Приложения:
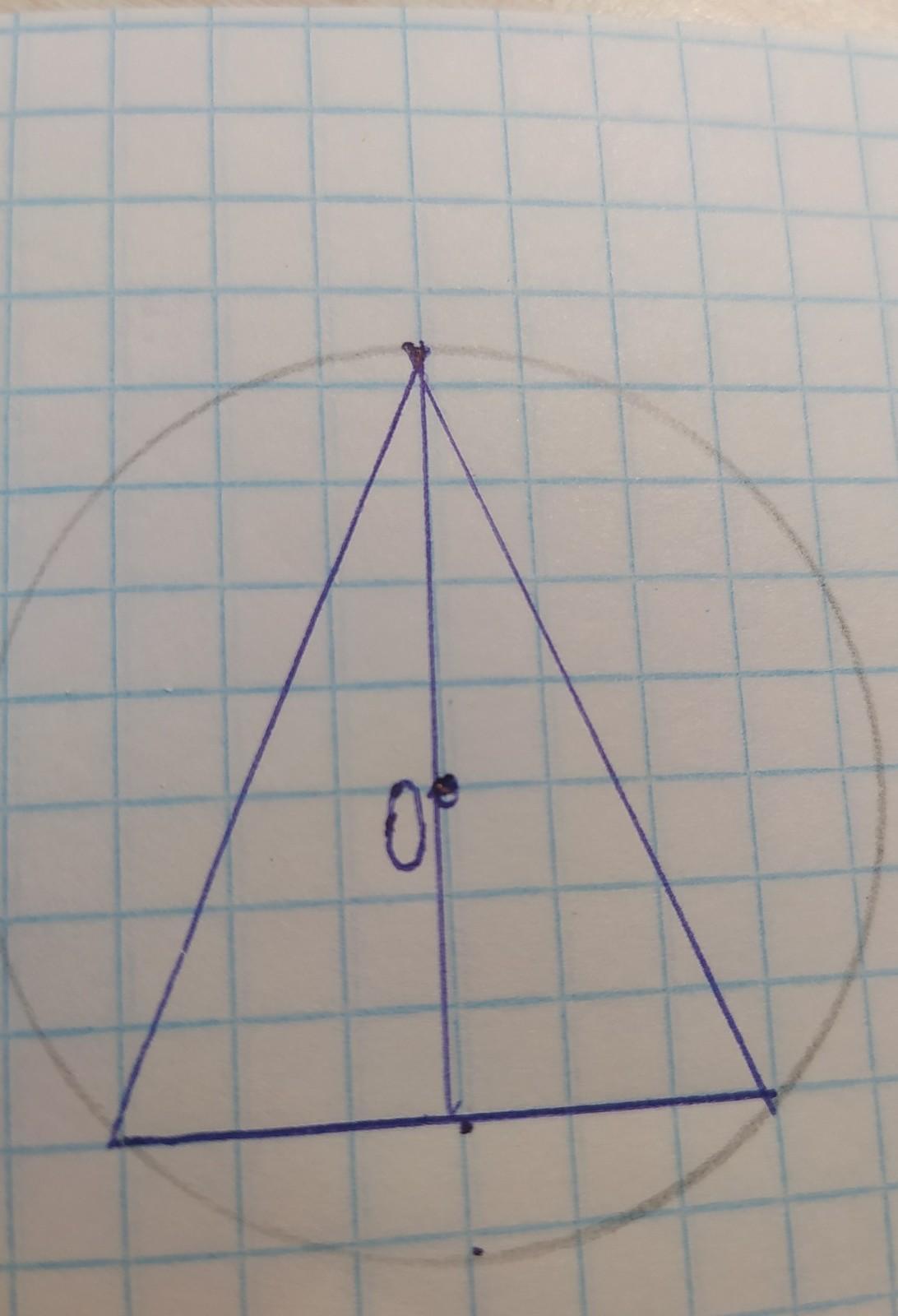
Ответы
Ответ дал:
1
Центр кола, яке вписане у трикутник, знаходиться у точці перетину серединних перпендикулярів.
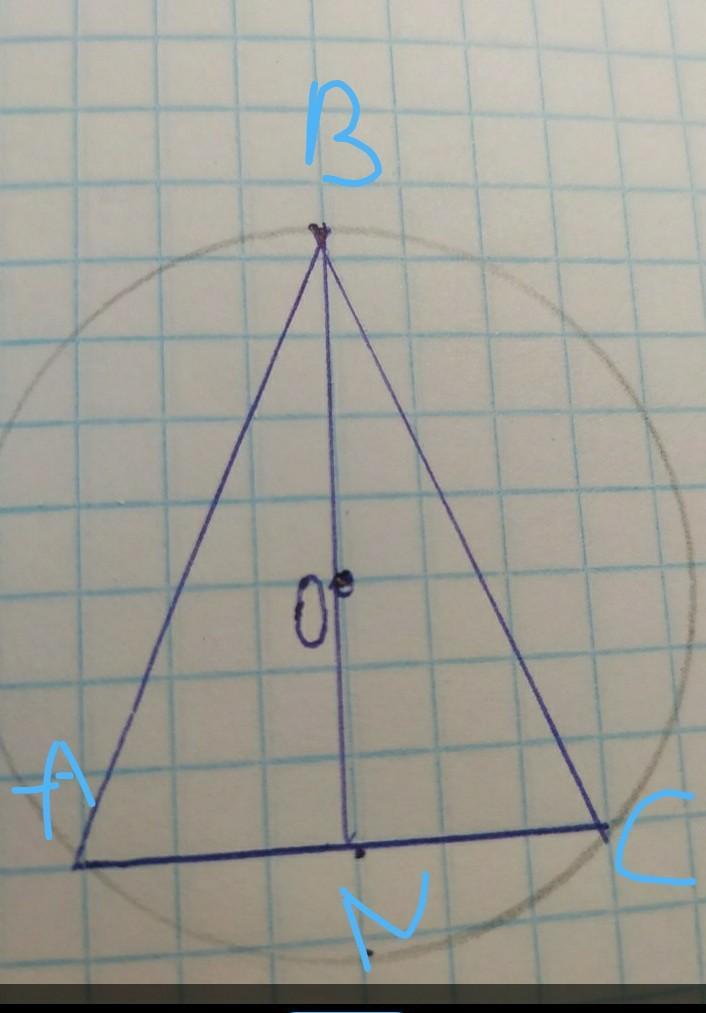
Отже, BN—серединний перпендикуляр відрізка АС.
AN=NC =>BN—медіана.
Якщо BN—медіана і висота, то з цього випливає, що трикутник ABC—рівнобедренний.
Приложения:
guvanch021272:
Точка пересечения биссектрис-центр вписанной окружности. В условии окружность описанная
Ответ дал:
1
Ответ:
Объяснение:
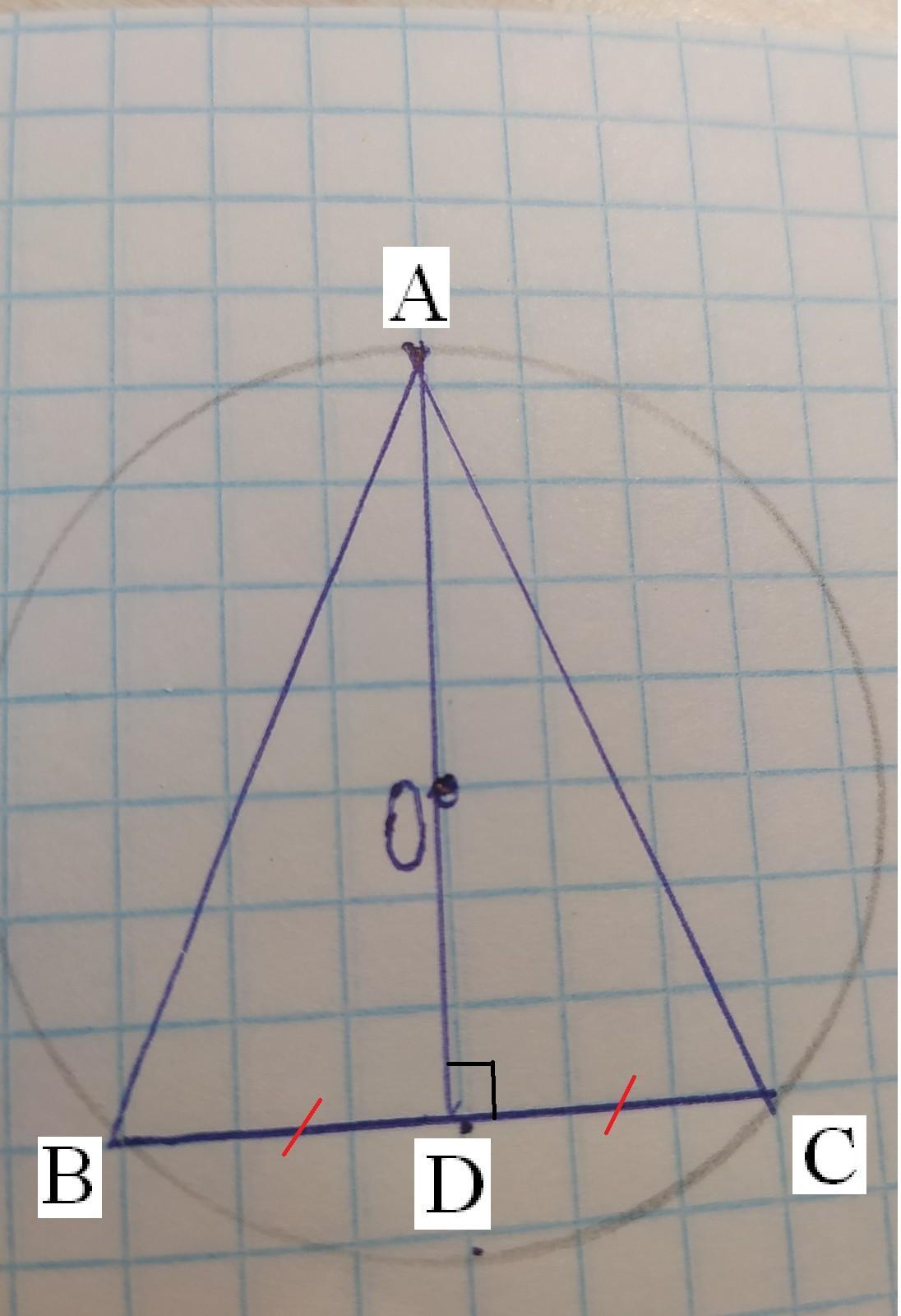
Центр окружности описанной около треугольника-точка пересечения серединных перпендикуляров его сторон.
AD⊥BC, O∈AD⇒AD-серединный перпендикуляр отрезка BC
Тогда BD=CD, значит AD-медиана
AD-медиана, AD-высота⇒ΔАBC-равнобедренный
ч.т.д.
Приложения:
Похожие вопросы
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад