найдите наименьшее целое значение a при котором абсцисса всех общих точек графика функции f(x)=a\x и g(x)=5\2x^2-2x отрицательна очень срочно!!!!

Ответ:

а= - 2.

Пошаговое объяснение:

Найдем абсциссы общих точек графика, решив уравнение:

ОДЗ:

Абсцисса всех общих точек отрицательна. Тогда составим неравенство.

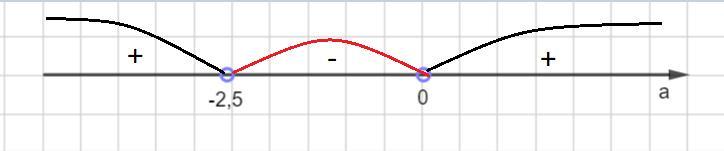
Решим данное неравенство методов интервалов. Отметим на координатной прямой точки -2,5 и 0 и определим знак на полученных интервалах.

Тогда

.

Так как  , то  

то таких значений а нет.

Значит, а∈ (-2,5; 0)

Тогда наименьшее целое значение а= - 2.