• Предмет: Алгебра
  • Автор: lunnaiapoxodka6
  • Вопрос задан 7 лет назад
< >

4.(дифференциальное исчисление )

выразите(вычислить производную?) следующую функцию:

Приложения:

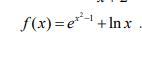
Ответы

Ответ дал: Matematiktm
1

Ответ:

y=e^{x^{2}-1} +lnx;\\y^{'} =(e^{x^{2}-1} +lnx)^{'}=(e^{x^{2}-1})^{'} +(lnx)^{'}=e^{x^{2}-1}(x^{2}-1})^{'}+\frac{1}{x} =e^{x^{2}-1}*2x+\frac{1}{x} =2xe^{x^{2}-1}+\frac{1}{x}

Объяснение:

Ответ дал: Vasily1975
0

Ответ: f'(x)=2*x*e^(x²-1)+1/x.

Объяснение:

f'(x)=[e^(x²-1)]'+[ln(x)]'=[e^(x²-1)]*(x²-1)'+1/x=2*x*e^(x²-1)+1/x

Похожие вопросы
Русский язык
1 год назад
20 баллов! Выпишите из художественных произведений ,изучаемых на уроках литературы ,5-6 простых предложений.
Русский язык
1 год назад
дети играли во дворе своего дома . словосочетания вместе с вопросами
Математика
2 года назад
Представьте в виде смешанного числа выражение ​
История
2 года назад
Соғыс жүргізу әдісі мен оның түсіндірмесі арасында дұрыс байланыс орнат. Бұл әдіс негізінен қазақ батырларының ордасы орналасқан таулы аймақта қолданылды. Қазақ батырларының тактикасы келесідей
Математика
8 лет назад
в бидон помещается 35 л молока А в стеклянную банку игрок литров Во сколько раз вместимость бидона больше вместимости банки
Математика
8 лет назад
Какую наибольшую сумму цифр можно получить на табло электронных часов показывающих только часы и минуты?
Математика
9 лет назад
фермер решил выделить под морковку - 3/20 горОда, под буряк - 4/20, под цыбулю - 6/20, под горошек - 2/20, под кортошку - 7/20. Сможет ли он реализовать свой план?
Алгебра
9 лет назад
найдите значение выражения: 8^11/4^17