Предмет: Алгебра
Автор: Reqiuem10
Вопрос задан 7 лет назад

< >

Решите..................

Приложения:

Reqiuem10: Я надеюсь здесь не надо использовать формулу Герона

Ответы

Ответ дал: NNNLLL54

2

Ответ:

$S=10\cdot 10-S_1-S_2-S_3=100-0,5\cdot 10\cdot 7-0,5\cdot 10\cdot 7-0,5\cdot 3\cdot 3=\\\\=100-70-4,5=25,5$

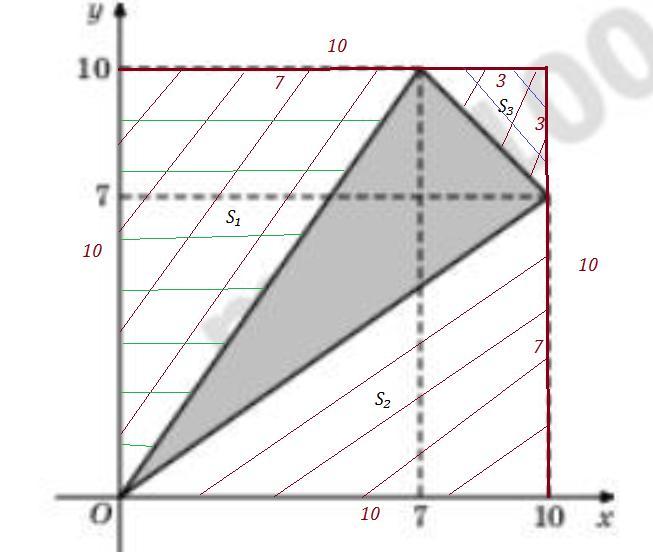
Из площади квадрата вычли площади трёх лишних прямоугольных треугольников. См. рисунок .

2 cпособ. Стороны треугольника АОВ равны:

$OA=\sqrt{OK^2+OB^2}=\sqrt{10^2+7^2}=\sqrt{149}\ ,\\\\OB=\sqrt{OC^2+AC^2}=\sqrt{7^2+10^2}=\sqrt{149}$

$\angle {AOB}=\angle {AOC}-\angle {BOK}=\alpha -\beta \\\\sin\angle {AOB}=sin(\alpha -\beta )=sin\alpha \cdot cos\beta -sin\beta \cdot cos\alpha =\\\\=\dfrac{AC}{OA}\cdot \dfrac{OK}{OB}-\dfrac{BK}{OB}\cdot \dfrac{OC}{OA}=\dfrac{10}{\sqrt{149}}\cdot \dfrac{10}{\sqrt{149}}-\dfrac{7}{\sqrt{149}}\cdot \dfrac{7}{\sqrt{149}}=\dfrac{100-49}{149}=\dfrac{51}{149}\\\\\\S_{AOB}=\dfrac{1}{2}\cdot OA\cdot OB\cdot sin\angle {AOB}=\dfrac{1}{2}\cdot \sqrt{149}\cdot \sqrt{149}\cdot \dfrac{51}{149}=\dfrac{51}{2}=25,5$

Приложения:

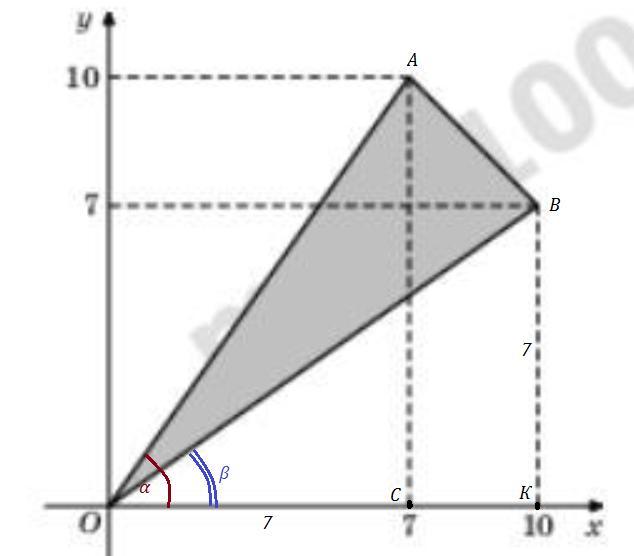
Reqiuem10: Можно обьеснения?

Reqiuem10: Есть другой вариант связный с Синиусом через кординаты или это дичь?)

NNNLLL54: зачем находить sin , если можно проще ??? можно и по формуле Герона найти , вычислив предварительно длины сторон треугольника .

Reqiuem10: Если скину можешь через синиус найти?просто не смог вспомнить как кординаты и синиус и сосиниу связывать между собой

NNNLLL54: сделаю, но позже

Reqiuem10: И sin и cos *

Reqiuem10: Я скину тогда , будет время решай.

NNNLLL54: написала

Reqiuem10: Красавчик.

NNNLLL54: njтогда отмечай ЛО

Похожие вопросы

Другие предметы

1 год назад

помогите пожалуйста сделать задание 3

Английский язык

1 год назад

complete they guestions. Then write answers.

История

2 года назад

1916 жылғы 25 маусымдағы патша жарлығына либерал-демократтарың көзқарасын талда. «Қазақ» газетінің төңірегіне біріккен либерал-демократияшыл зиялылардың жетекшілері (А.Байтұрсынов, Ә.Бөкейханов,

История

2 года назад

написать эссе "Какую роль играли батыры в казахском обществе, назвать имена известных батыров".ПОЖАЛУЙСТА

Математика

8 лет назад

545 подалуйстаааааа!!!!!!!!!! Умоляю !!!!

Математика

8 лет назад

Там надо выбирать варианты помогите и подчеркнуть

Математика

9 лет назад

2 1/3+4 1/10:(2 7/15-5/12)*5/6

Обществознание

9 лет назад

Подбери примеры к каждому виду норм: обычаи,традиции, нормы морали, правовые нормы, религиозные нормы, политические нормы, эстетические нормы.