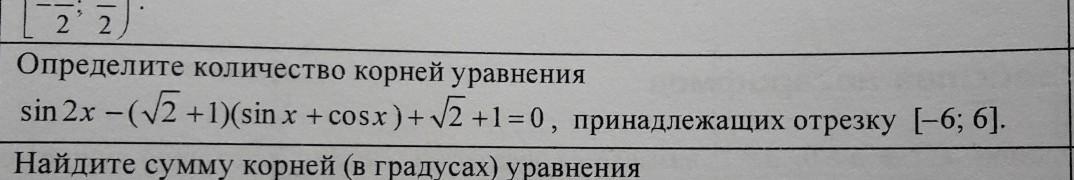Предмет: Алгебра
Автор: iriska567
Вопрос задан 7 лет назад

ПОМОГИТЕ РЕШИТЬ ЭТО ЗАДАНИЕ ПОЖАЛУЙСТА, ответ 5

Приложения:

Ответы

Ответ дал: NNNLLL54

Ответ:

$sin2x-(\sqrt2+1)(sinx+cosx)+\sqrt2+1=0\ \ ,\ \ x\in [-6\ ;\ 6\ ]\\\\2sinx\cdot cosx-(\sqrt2+1)(sinx+cosx)+\sqrt2+1=0\\\\Zamena:\ \ t=sinx+cosx\ ,\\\\t^2=(sinx+cosx)^2=\underbrace{sin^2x+cos^2x}_{1}+2sinx\cdot cosx=1+2sinx\cdot cosx\ \ ,\\\\2sinx\cdot cosx=t^2-1\ \ \Rightarrow \ \ \ sinx\cdot cosx=\dfrac{t^2-1}{2}\\\\\\t^2-1-(\sqrt2+1)\cdot t+\sqrt2+1=0\ ,\\\\t^2-(\sqrt2+1)\cdot t+\sqrt2=0\ \ ,\\\\D=(\sqrt2+1)^2-4\cdot \sqrt2=(2+2\sqrt2+1)-4\sqrt2=2-2\sqrt2+1=(\sqrt2-1)^2$

$\sqrt{D}=\sqrt{(\sqrt2-1)^2}=|\sqrt2-1|=\sqrt2-1\\\\t_1=\dfrac{(\sqrt2+1)-(\sqrt2-1)}{2}=1\ \ ,\ \ t_1=\dfrac{(\sqrt2+1)+(\sqrt2-1)}{2}=\sqrt2\\\\a)\ \ sinx+cosx=1\ |:\sqrt2\\\\\dfrac{1}{\sqrt2}\cdot sinx+\dfrac{1}{\sqrt2}\cdot cosx=\dfrac{1}{\sqrt2}\\\\cos\dfrac{\pi}{4}\cdot sinx+sin\dfrac{\pi }{4}\cdot cosx=\dfrac{1}{\sqrt2}\\\\sin\Big(x+\dfrac{\pi}{4}\Big)=\dfrac{1}{\sqrt2}\\\\x+\dfrac{\pi}{4}=\dfrac{\pi}{4}+2\pi n\ \ \ ili\ \ \ x+\dfrac{\pi}{4}=\dfrac{3\pi}{4}+2\pi n\ \ ,\ n\in Z$

$x_1=2\pi n\ \ \ ili\ \ \ x_2=\dfrac{\pi}{2}+2\pi n\ \ ,\ n\in Z$

$x_1\in [-6\ ;\ 6\ ]:\ \ 6\ rad\approx 344^\circ \ \ ,\ \ x_1\in [-344^\circ \ ;\ 344^\circ ]\\\\x_1=360^\circ \cdot n\ \ ,\\\\n=0\ \ \to \ \ x_1=0\in [-6;6\ ]\\\\\ \ x_2=\dfrac{\pi }{2}+2\pi n=90^\circ +360^\circ n\ ,\\\\n=-1\ \ \to \ \ x_2=-270^\circ=-\dfrac{3\pi}{2}\in [-6;6\ ]\\\\n=0\ \ \to \ \ x_2=90^\circ =\dfrac{\pi}{2}\in [-6;6\ ]$

При других значениях n корни не будут входить в указанный промежуток .

$b)\ \ sinx+cosx=\sqrt2\ |:\sqrt2\\\\\dfrac{1}{\sqrt2}\cdot sinx+\dfrac{1}{\sqrt2}\cdot cosx =1\\\\sin\Big(x+\dfrac{\pi}{4}\Big)=1\ \ \ \Rightarrow \ \ \ x+\dfrac{\pi}{4}=\dfrac{\pi}{2}+2\pi k\ \ ,\ \ x=\dfrac{\pi}{4}+2\pi k\ ,\ k\in Z\\\\x=45^\circ +360^\circ k\\\\k=-1\ \ \to \ \ x=-315^\circ =-\dfrac{7\pi}{4}\in [-6;6\ ]\\\\k=0\ \ \to \ \ x=45^\circ =\dfrac{\pi}{4}\in [-6;6\ ]$

При других значениях k корни не будут входить в указанный промежуток .

$Otvet:\ 1)\ x_1=2\pi n\ ,\ x_2=\dfrac{\pi}{2}+2\pi n\ ,\ x_3=\dfrac{\pi}{4}+2\pi k\ \ ,\ \ n,k\in Z\ ;\\\\{}\ \ \ 2)\ \ x\in [-6;6\ ]\ \ \Rightarrow \ \ x=0\ ;\ -\dfrac{7\pi}{4}\ ;\ -\dfrac{3\pi}{2}\ ;\ \dfrac{\pi}{4}\ ,\ \dfrac{\pi}{2}\ ;\ \ vsego\ 5 \ kornej\ .$

iriska567: а как это так получилось с заменой

NNNLLL54: что значит "как получилось с заменой" ??? вот заменили сумму на новую переменную, и всё получилось ... учи приёмы решения уравнений , а за ответ можно и спасибо нажать

Похожие вопросы

Английский язык

1 год назад

Напиши предложения в отрицательной форме +not .We are a big family. He is a good student. He is a swimmer.

Русский язык

1 год назад

Какое слово нужно выбрать, чтобы в словосочетании была связь ПРИМЫКАНИЕ? Её.... 1)вопросы 2)спросить

Алгебра

2 года назад

Помогите пожалуйста дам 35 балов

Қазақ тiлi

2 года назад