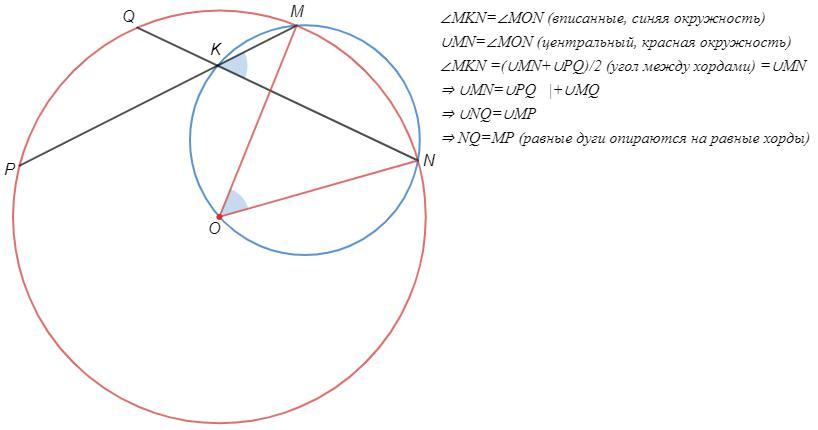
В окружности Ω с центром O выбрана произвольная точка K внутри и произвольная точка M на самой окружности. Через точки O, K , M проведена окружность, которая второй раз пересекает Ω в точке N. Хорды окружности Ω MP и NQ пересекаются в точке K. Доказать, что они равны.

cos20093: Точка T снаружи от красной окружности. Теперь откуда я взял эту задачку. У кого есть задачник Шарыгин и Гордин 5000 задач по геометрии, там есть номер 3393. Я никак не мог сообразить, откуда там подобие треугольников, пока не выделил вот эту задачу как отдельное утверждение. Тогда все моментально решилось.

cos20093: "Если провести линию центров до пересечения с красной (на чертеже выше) окружностью в точке T" пардон, как раз с синей :)))

cos20093: Еще раз - точка T на СИНЕЙ окружности.

yugolovin: Доказательство автора решени я мне показалось вполне корректным и простым

cos20093: и мне :)

cos20093: В этой простенькой задачке есть один очень интересный момент. Точки М и К - произвольные, у второй окружности есть только одна фиксированная особенность - она проходит через центр первой. И хорды получаются равными. Поэтому я шел "по другой лестнице" рассуждений - решение должно было показать со всей ясностью, причем тут центр. А так-то решение совершенно правильное, у меня и в мыслях не было спорить :).

siestarjoki: Решение 3393 https://i.imgur.com/4KyRPvE.png

siestarjoki: Хорошая задача, видны разные пути решения