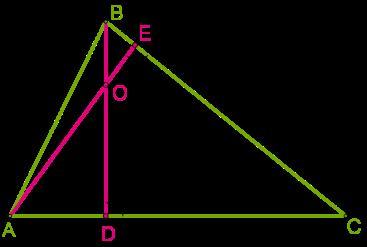
Высоты треугольника пересекаются в точке O.
Величина угла ∡ BAC = 84°, величина угла ∡ ABC = 87°.
Определи угол ∡ AOB.

∡ AOB =
°.

Ответ:

∠АОВ = 171°

Объяснение:

Дано:

∠ВАС = 84°

∠АВС = 87°

О - ортоцентр ΔАВС

Найти:

∠АОВ

Решение:

В ΔАВС по свойству углов треугольника

∠АСВ = 180° - (∠ВАС + ∠АВС) = 180° - (84° + 87°) = 9°

Сумма внутренних углов выпуклого четырёхугольника CDOE равна 360°.

∠СEO = ∠CDO = 90° (так как АЕ и BD -высоты)

∠DCE = ∠АСВ = 9°

Тогда

∠DOE = 360° - (∠DCE + ∠СEO + ∠CDO) = 360° - (9° + 90° + 90°) = 171°

∠АОВ = ∠DOE = 171° (так как ∠АОВ и ∠DOE - вертикальные углы)