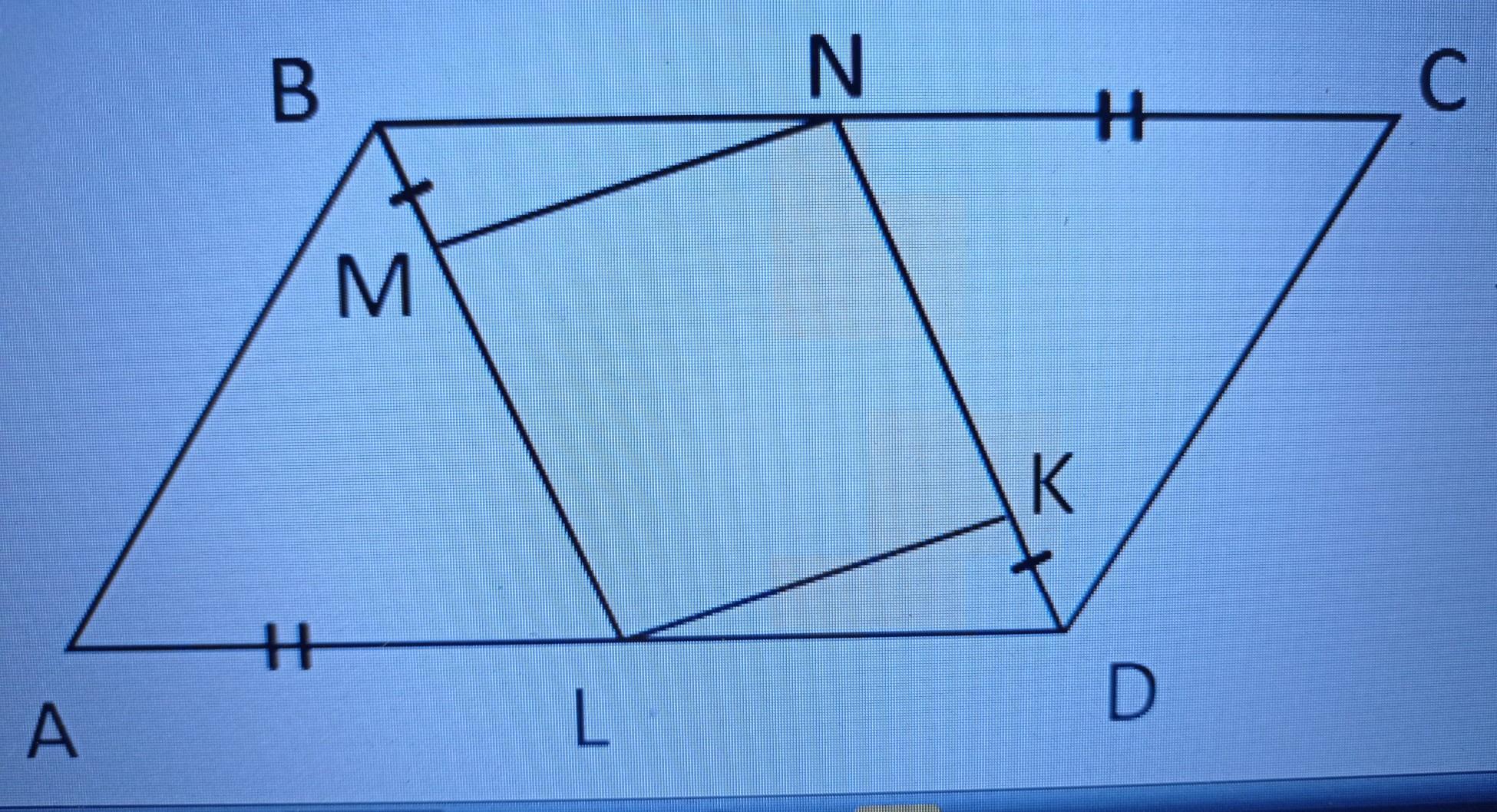
На рисунку MNKL - паралелограм. Доведіть, що чотирикутник ABCD також є паралелограмом. ​

Объяснение:

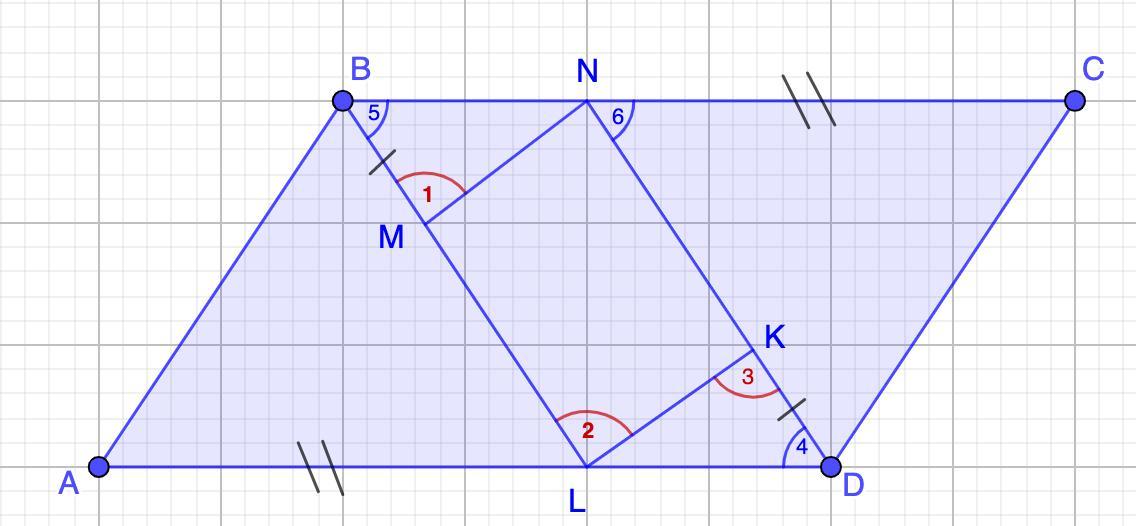
Дано: MNKL - параллелограмм.

AL=NC; BM=KD.

Доказать: ABCD - параллелограмм.

Доказательство:

MNKL - параллелограмм. ⇒ MN║KL  и ML║NK.

1) Рассмотрим ΔMBN и ΔLKD.

KD=MB (по условию)

MN=LK (свойство параллелограмма)

∠1=∠2 (соответственные при NM║LK и секущей BL.

∠3=∠2 (накрест лежащие при LB║ND и секущей LK.

⇒∠1=∠3.

ΔMBN и ΔLKD (по двум сторонам и углу между ними, 1 признак)

⇒ LD=BN; ∠5=∠4 (как соответственные элементы)

2) AD=AL+LD

  BC=BN+NC

⇒AD=BC

3) ∠5=∠4 (п.1)

  ∠5=∠6 (соответственные при BL║DN и секущей ВС)

⇒∠4=∠6 - накрест лежащие при ВС и AD и секущей ND;

⇒ ВС ║ AD.

4) AD=BC (п.2)

   ВС ║ AD (п.3)

Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник - параллелограмм.

⇒ABCD - параллелограмм