Нужно найти сумму S бесконечно убывающей геометрической прогрессии, заранее благодарен
Приложения:
Ответы
Ответ дал:
1
Ответ:
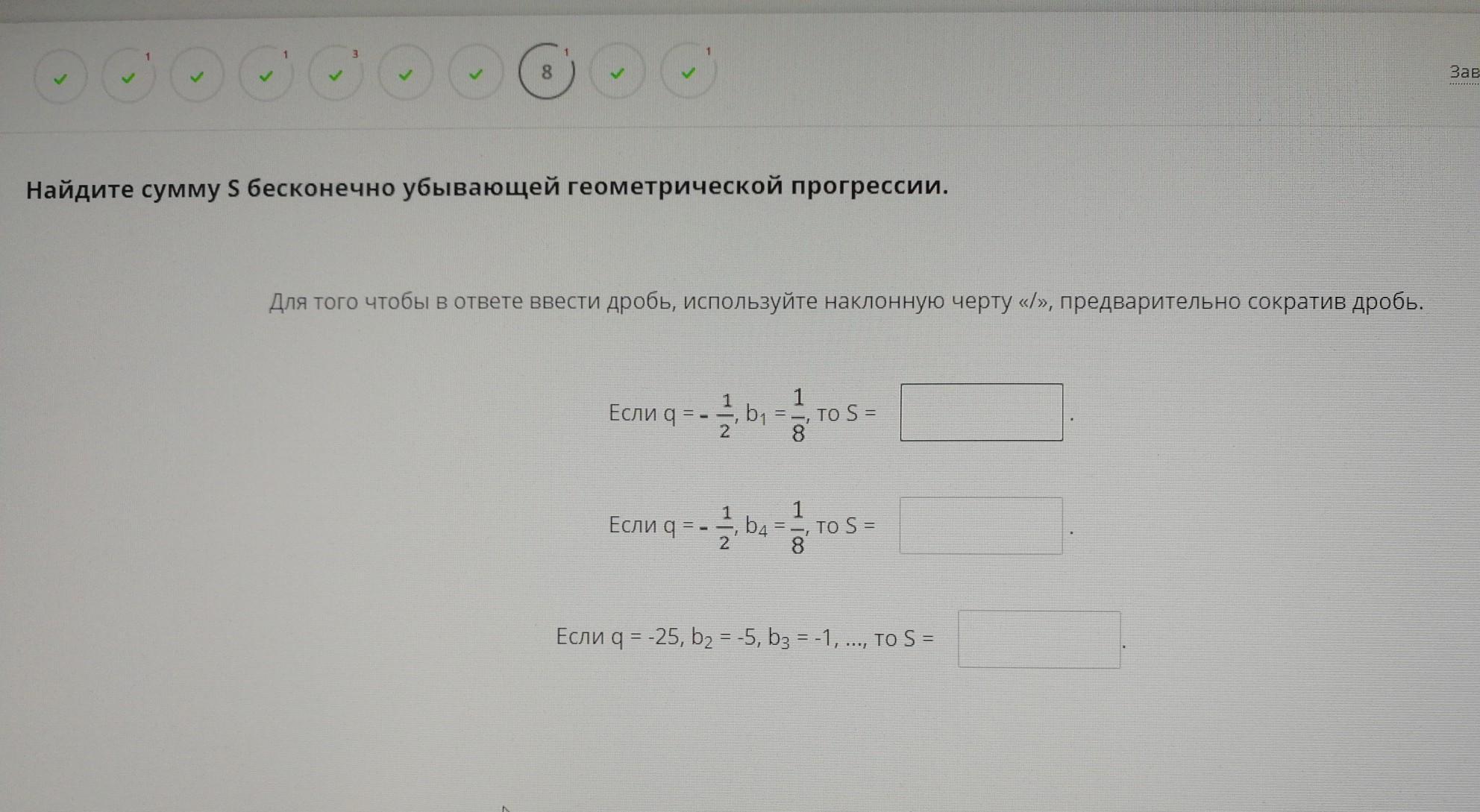
1) 1 / 12
2) - 2 / 3
3) - 1 / 16250
Объяснение:
b1 = 1/8
q = -0.5
Сначала нужно найти b1
bn = b1*q^(n-1) = b4 = b1 * q^(4-1)
b1 = b4 / q^3 = 1/8 / (-0.5)^3 = -1
Также находим b1. Он равняется
kallivan51:
спасибо, но я уже сам решил)
у вас последнее неверно
получится -31,25
может кому пригодится
Похожие вопросы
1 год назад
1 год назад
2 года назад
8 лет назад
9 лет назад