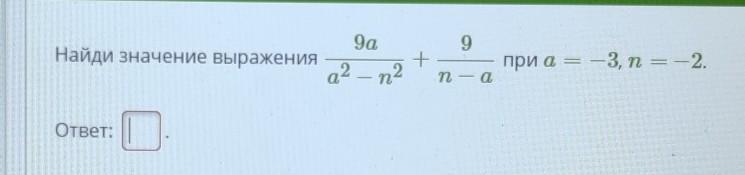Предмет: Алгебра
Автор: buriamw0152
Вопрос задан 7 лет назад

< >

помогите плиззз,срочнооооо!!!!!!

Приложения:

Ответы

Ответ дал: zidane90

0

Ответ:

Объяснение:

$\frac{9a}{a^2-n^2}+ \frac{9}{n-a}=$

Умножим числитель и знаменатель второй дроби на (-1):

$\frac{9a}{a^2-n^2}+ \frac{(-1)*9}{(-1)(n-a)}= \frac{9a}{(a-n)(a+n)}- \frac{9}{a-n}=$

Приведем к общему знаменателю:

$\frac{9a}{(a-n)(a+n)}- \frac{9}{a-n}= \frac{9a-9(a+n)}{(a-n)(a+n)}= \frac{9a-9a-9n}{(a-n)(a+n)}=\frac{-9n}{(a-n)(a+n)}=\frac{-9*(-2)}{(-3+2)*(-3-2)}=\frac{18}{(-1)*(-5)}=\frac{18}{5}$

Ответ дал: СовушкинДомик

0

Ответ:

Если а=-3, n=-2, то:

$\frac{9a}{ {a}^{2} - {n}^{2} } + \frac{9}{n - a} = \frac{9 \times ( - 3)}{ { (- 3)}^{2} - {( - 2)}^{2} } + \frac{9}{ - 2 - ( - 3)} = \frac{ - 27}{9 - 4} + \frac{9}{1} = - \frac{27}{5} + 9 = - 5.4 + 9 = 3.6$

Похожие вопросы

Русский язык

1 год назад

Синквейн на тему синтаксис

Английский язык

1 год назад

переведите правильно плиз.

Другие предметы

2 года назад

Органические продукты питания это правда или миф?

Математика

2 года назад

Милю бога, уже кидаю раз 4 никто не хочет написать эти 3 задачи, пожалуйста, помогите((

Математика

8 лет назад

Упростить: 8(4а-3b+11c); (16x+14y-23z)*15

Математика

8 лет назад

Задание номер 8 и 9 пожалуйста помогите решать с x

Алгебра

9 лет назад

помогите, пожалуйста! 1. log2 sin x/2 < -1 2. log1/2 cos 2x > 1

Биология

9 лет назад

СКОЛЬКО ХРОМОСОМ СОДЕРЖИТ САМАТИЧЕСКИЕ КЛЕТКИ КОЖИЦЫ КАРТОФЕЛЯ, ЕСЛИ ИХ ДОЧЕРНИЕ КЛЕТКИ, ОБРАЗОВАВШИЕСЯ ПРИ НЕПРЯМОМ ДЕЛЕНИИ, ИМЕЮТ 48 ХРОМОСОМ? 1) 12 2)24 3)48 4)92