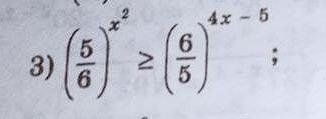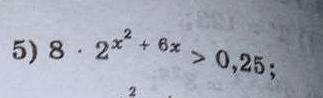Предмет: Алгебра
Автор: Miа16
Вопрос задан 7 лет назад

Алгебра. Даю 20 баллов. Решить 2 уравнения. С подробным решением.

Приложения:

Ответы

Ответ дал: Universalka

$3)\Big(\dfrac{5}{6} \Big)^{x^{2} }\geq\Big(\dfrac{6}{5}\Big)^{4x-5} \\\\\\\Big(\dfrac{5}{6} \Big)^{x^{2} }\geq\Big(\dfrac{5}{6}\Big)^{5-4x}\\\\\\0<\dfrac{5}{6}<1 \ \Rightarrow \ x^{2} \leq5-4x\\\\\\x^{2}+4x-5\leq 0\\\\(x-1)(x+5)\leq0$

+ + + + + [-5] - - - - - [1] + + + + +

//////////////////

Ответ : x ∈ [ - 5 ; 1]

$5) \ 8\cdot2^{x^{2}+6x } >0,25\\\\2^{3}\cdot2^{x^{2}+6x }>2^{-2} \\\\2^{x^{2}+6x+3 }>2^{-2}\\\\2>1 \ \Rightarrow \ x^{2}+6x+3>-2\\\\x^{2}+6x+5>0\\\\(x+1)(x+5)>0$

+ + + + + (-5) - - - - - (-1) + + + + +

///////////// //////////////

Ответ : x ∈ (- ∞ ; -5) ∪ (-1 ; + ∞)

Universalka: Да, опечатка, уже исправила . Умница !!!

Miа16: умница это вы :)

Miа16: ещё вопросик, к примеру 5, вот я нашла точки -5 и 1, нарисовала прямую, подставила значения, получилось по бокам + и +, а в середине - , только как теперь получить то что вы написали в скобках как ответ?

Miа16: простите если напрягаю с вопросамии

Universalka: Неравенство со знаком > , значит ответы там где плюсы, а если бы неравенство было со знаком < , то ответы были бы там где минусы .

Miа16: всё, поняла)))))))))

Miа16: большое вам спасибо :)

Universalka: Всегда рада помочь хорошему человеку :)

Miа16: :)

Miа16: Я сделала ещё вопросик, есть время на него?

Похожие вопросы

Русский язык

1 год назад

найти загадку,слово-отгадка в которой содержит парный мягкий согласный звук

Другие предметы