ПОМОГИТЕ, ПОЖАЛУЙСТА!!!
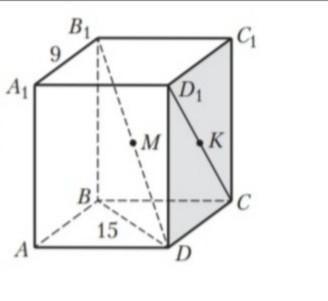
Дан прямоугольный параллелепипед ABCDA1B1C1D1, A1B1=9, BD=15, точки М и К - середины отрезков B1D и D1C. Найдите длину отрезка МК​

Ответ:

Угол, под которым пересекается прямая MN с верхней плоскостью куба, равен углу, под которым эта прямая пересекается с нижней плоскостью куба в силу параллельности этих плоскостей.

a - ребро куба

BM = 1/2*BD = a√2/2 = a/√2

BN = 1/2*a

tg(∠BMN) = BN/BM = 1/2*a / (a/√2) = √2/2 = 1/√2

В ответе требуют квадрат тангенса

tg²(∠BMN) = (1/√2)² = 1/2

Объяснение:

Ответ:

длина отрезка МК равна 60