помогите алгебра 4.1 просьба не знаете не пишите

Приложения:

Ответы

Ответ дал: Vopoxov

Ответ:

1) -20;

2) 21;

3) 28;

4) 22;

5) 1;

6) 3.

Объяснение:

См. на приложенном фото.

Приложения:

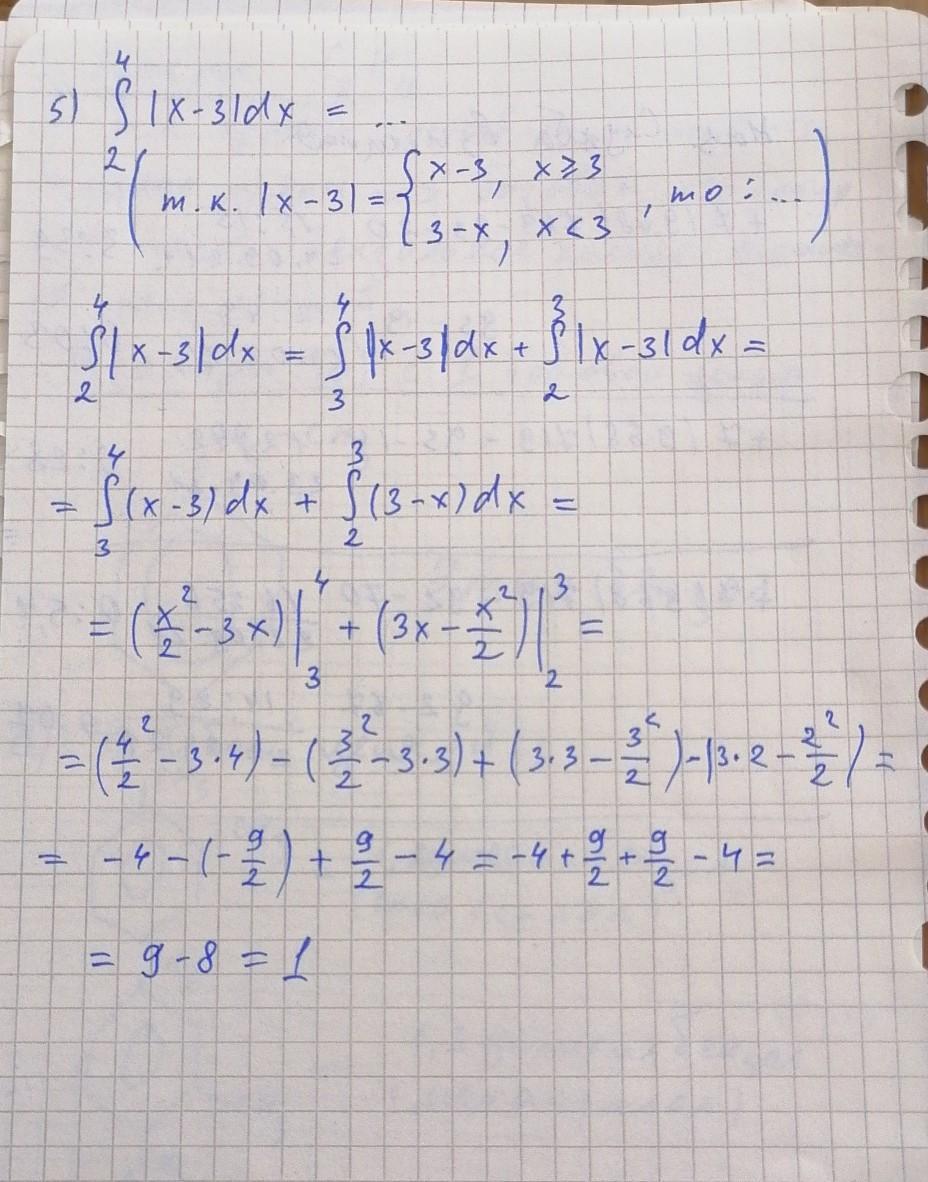
Vopoxov: Оставшееся, сорри, не успеваю. М.б. смогу дополнить после 18:30 по МСК

77112300: ок

kazemir4ik: там с модулем, они тяжелее)))

77112300: сможешь решить??

kazemir4ik: не, врядли...

kazemir4ik: пока на ум ничего не приходит

77112300: Vopoxov когда сможете доделать задание

Ответ дал: NNNLLL54

Ответ:

$1)\ \ \displaystyle \int\limits^2_{-3}\, (2x-3)\, dx=\frac{(2x-3)^2}{2\cdot 2}\Big|_{-3}^2=\frac{1}{4}\cdot \Big(1^2-(-9)^2\Big)=-20\\\\\\2)\ \ \int\limits^1_{-2}(5-4x)\, dx=\frac{(5-4x)^2}{-4\cdot 2}\Big|_{-2}^1=-\frac{1}{8}\cdot \Big(1^2-13^2\Big)=21\\\\\\3)\ \ \int\limits^0_{-2}\, (3x^2+10)\, dx=\Big(x^3+10x\Big)\Big|_{-2}^0=-\Big((-2)^3-20\Big)=28$

$\displaystyle 4)\ \ \int\limits^2_0(6x^2-2x+5)\, dx=(2x^3-x^2+5x)\Big|_0^2=16-4+10=22\\\\\\5)\ \ \int\limits^4_2\, |x-3|\, dx=\int\limits^3_2\, (3-x)\, dx+\int\limits^4_3\, (x-3)\, dx=-\frac{(3-x)^2}{2}\Big|_2^3+\frac{(x-3)^2}{2}\Big|_3^4=\\\\\\=-0+\frac{1}{2}+\frac{1}{2}-0=1$

$\displaystyle 6)\ \ \int\limits^2_0\, (x+|x-1|)\, dx=\int\limits^1_0\, (x-(x-1)\ )\, dx+\int\limits^2_1\, (x+(x-1)\ )\, dx=\\\\\\=\int\limits^1_0\, dx+\int\limits^2_1\, (2x-1)\, dx=x\Big|_0^1+\frac{(2x-1)^2}{2\cdot 2}\Big|_1^2=(1-0)+\frac{1}{4}\cdot ( 3^2-1^2)=\\\\\\=1+2=3$