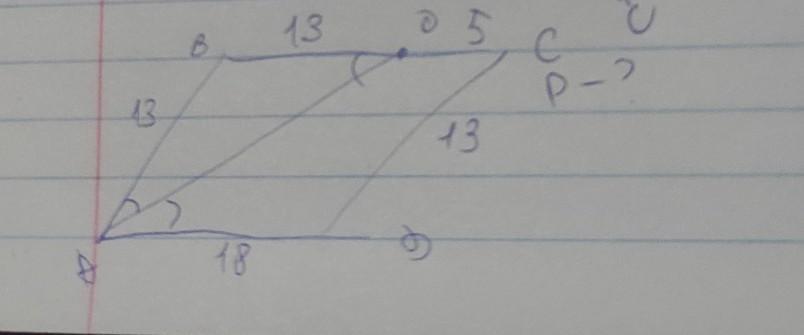
В параллелограмме ABCD биссектриса АО угла А делит строну BC на отрезки BO=13 и OC=5. Найти периметр параллелограмма

Ответ:

62

Объяснение:

P.s. рисунок грубо говоря, никудышный, по идее там все ровненько должно быть)

AO - биссектриса, следовательно, <BAO=<OAD.

углы <BOA и <OAD - соответственные, проще говоря, они равны. Соответственно, если углы <BOA и <OAD равны, а угол <OAD в свою очередь равен углу <BAO, то и углы <BOA и <BOA равны, тогда треугольник ABO - равнобедренный, откуда: BO=AB=13. Ну и по свойству параллелограмма противолежащие стороны равны друг другу: AB=CD=13, BC=AD=13+5=18

Находим периметр: