Предмет: Алгебра
Автор: Аноним
Вопрос задан 7 лет назад

Найти общее решение или общий интеграл дифференциального уравнения.
Решить задачу Коши.

Приложения:

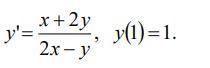
Ответы

Ответ дал: NNNLLL54

Ответ:

$y'=\dfrac{x+2y}{2x-y}\ \ ,\ \ y(1)=1\\\\\\y'=\dfrac{1+2\cdot \frac{y}{x}}{2-\frac{y}{x}}\ \ ,\ \ \ t=\frac{y}{x}\ \ ,\ \ y=tx\ \ ,\ \ y'=t'x+t\\\\\\t'x+t=\dfrac{1+2t}{2-t}\ \ ,\ \ \ t'x=\dfrac{1+2t-2t+t^2}{2-t}\ \ ,\ \ t'x=\dfrac{t^2+1}{2-t}\ \ ,\\\\\\\dfrac{x\, dt}{dx}=-\dfrac{t^2+1}{t-2}\ \ ,\displaystyle \ \ \int \dfrac{(t-2)\, dt}{t^2+1}=-\int \dfrac{dx}{x}\ \ ,\\\\\\\frac{1}{2}\int \dfrac{2t\, dt}{t^2+1}-2\int \frac{dt}{t^2+1}=-\int \dfrac{dx}{x}\ \ ,$

$\displaystyle \frac{1}{2}\, ln(t^2+1)-2\, arctgt=-ln|x|+C\\\\\\\displaystyle \frac{1}{2}\, ln(\frac{y^2}{x^2}+1)-2\, arctg\frac{y}{x}=-ln|x|+C\ \ -\ \ obshij\ integral\\\\\\y(1)=1:\ \ \frac{1}{2}\, ln2-2arctg1=-ln1+C\\\\\frac{1}{2}\, ln2-2\cdot \frac{\pi}{4} =C\ \ \to \ \ \ C=\frac{ln2-\pi }{2}\\\\\\ \frac{1}{2}\, ln(\frac{y^2}{x^2}+1)-2\, arctg\frac{y}{x}=-ln|x|+\frac{ln2-\pi }{2}$