Ответы
Ответ дал:
1
Ответ:
Похожие вопросы
1 год назад
1 год назад
2 года назад
2 года назад
8 лет назад
8 лет назад
9 лет назад
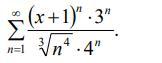
https://znanija.com/task/45813933