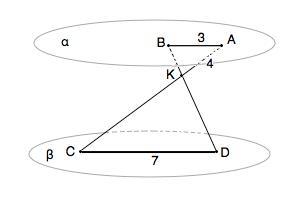
Точки А и В лежат в плоскости α, а точки C и D – в плоскости β, при этом плоскости α и β параллельны. Отрезки AC и BD пересекаются в точке K.

а) Докажите, что ΔAKB ~ ΔCKD

б) Найдите длину отрезка КС, если АВ = 3 см, CD = 7 см, АК = 4 см

Ответ: 9 ¹/₃ см.

Объяснение:    

     Из аксиомы о свойствах плоскости: через две пересекающиеся прямые можно провести одну и только одну плоскость. Следовательно, AC и CD лежат в одной плоскости.

     Если две параллельные плоскости пересекаются третьей, то линии их пересечения параллельны.

 Так как АВ|║CD, накрестлежащий углы при их пересечении секущими АС и BD равны. Два угла  треугольника  AKB равны двум углам треугольника CKD ⇒ ∆ AKB~ ∆ CKD по первому признаку.

      Из подобия следует отношение АВ:CD=AK:KC. ⇒

KC=CD•AK:AB=7•4:3=9 ¹/₃ см.