Дано:
Угол1 равен углу 2
Доказать:
Угол ВАС+ угол АСД=180°​

Ответ:

Что и требовалось доказать!

Объяснение:

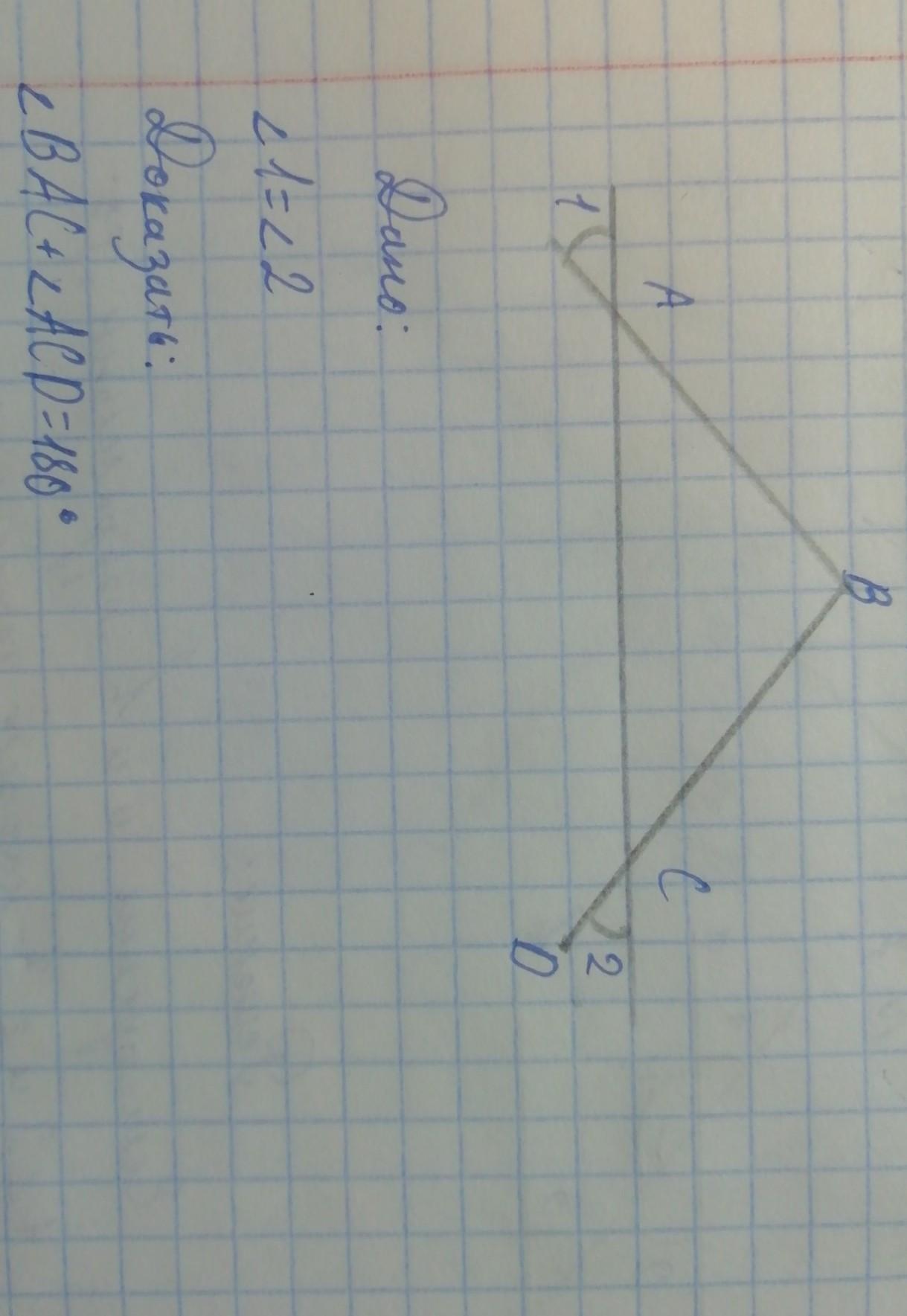
\angle 1, \angle BAC - вертикальные и поэтому равны.

\angle 2, \angle BCA - вертикальные и поэтому равны.

А так как \angle 1 = \angle 2, по условию \Rightarrow \angle BAC = \angle BCA

\Rightarrow \triangle ABC - равнобедренный.

\angle BCA + \angle ACD = 180^{\circ}, так как они смежные.

А так как \angle BCA = \angle BAC \Rightarrow \angle BAC + \angle ACD = 180^{\circ}.

думаю так если не правильно не верите меня

Объяснение:

<1=<2

<1=<ВАС как вертикальные

<2=<ВСА как вертикальные

<1=<2,значит <ВАС=<ВСА,

<ВСА+<АСD=180,т. к <ВСА=<ВАС, то

<ВАС+<АСD=180 градусов