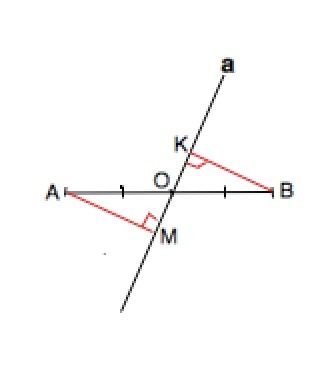
прямая a пересекает отрезок AB в точке O являющейся серединой отрезка AB. Докажите,
что точки A и B находятся на одинаковом расстоянии от прямой a .

Расстояние от точки до прямой измеряется длиной отрезка,  опущенного из точки на прямую перпендикулярно ей.

Опустим из А и В перпендикуляры АМ и ВК  на прямую а. 

∆ АМ и ∆ ВКО - имеют равные гипотенузы и равные (вертикальные) острые углы при О. 

Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.

Следовательно, АМ=ВК, что и требовалось доказать.