C
A
D
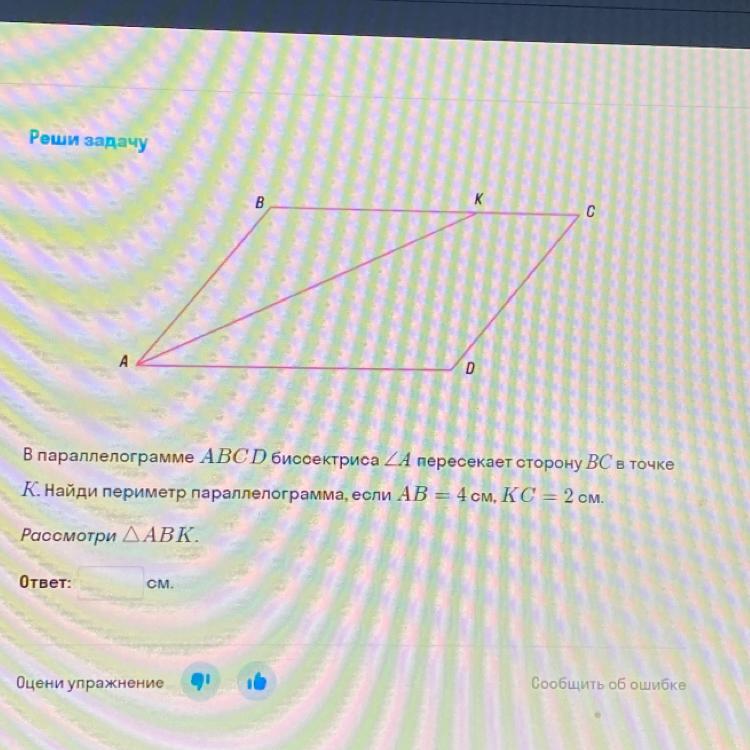
В параллелограмме ABCD биссектриса ZA пересекает сторону ВС в точке
К. Найди периметр параллелограмма, если AB = 4 см, КС = 2 см.
Рассмотри ДAВК.
Ответ:
СМ.

Ответ:

20 см

Объяснение:

по свойству, биссектриса в параллелограмме делит угол пополам и отсекает равнобедренный треугольник, отсюда следует что AB=BK= 4 см, а BC=BK+KC=4+2=6 см,

P= 2(a+b) = 2*(6+4)=20 см

Объяснение:

<ВАК=<КАD, т. к АК-биссектриса.

<КАD=<АКВ- при параллельных ВС и АD и секущей АК, значит тр-к АВК-равнобедренный, т. к <ВАК=<АКВ, значит АВ=ВК=4 см.

Тогда ВС=ВК+КС=4+2=6 см

АВ=СD=4 cм

ВС=АD=6 cм

Р=2(АВ+ВС)=2×(4+6)=20 см