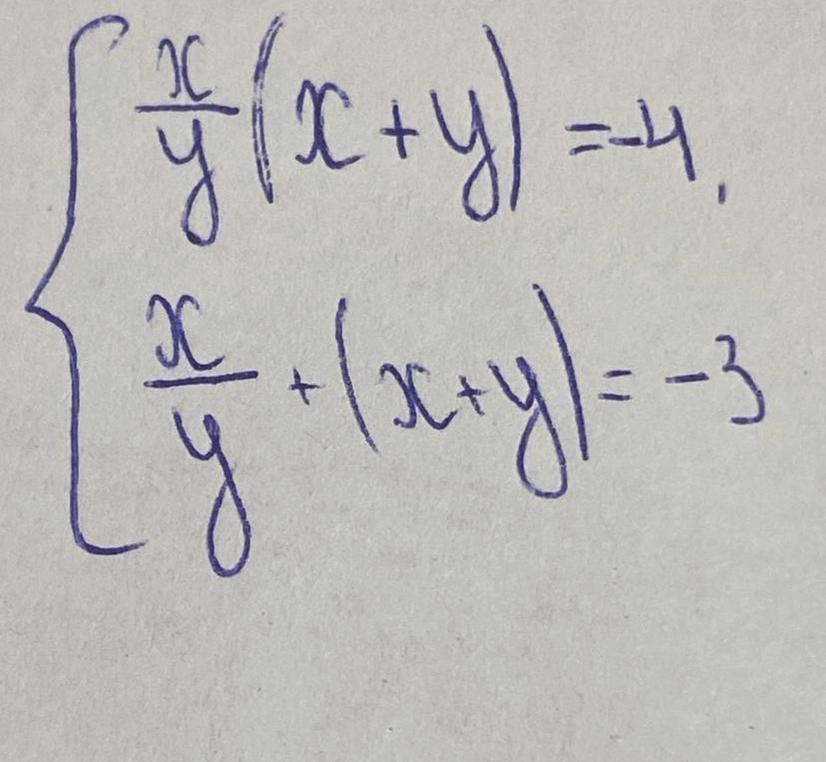Предмет: Алгебра
Автор: ozokjl
Вопрос задан 7 лет назад

< >

срочно, решить систему нелинейных уравнений!!

Приложения:

Ответы

Ответ дал: Alexandr130398

2

Ответ:

(-2;-2); (4/3; -1/3)

Объяснение:

сделаем замену:

x/y=t; x+y=k, тогда

$\left\{\begin{matrix} tk=-4 \\ t+k=-3 \end{matrix}\right. \ \Leftrightarrow \ \left\{\begin{matrix} (-3-k)k=-4 \\ t=-3-k \end{matrix}\right. \ \Leftrightarrow \ \left\{\begin{matrix} -3k-k^2=-4 \\ t=-3-k \end{matrix}\right.$

Решаем отдельно первое уравнение:

$-3k-k^2=-4 \\ k^2+3k-4=0 \\ k_1=-4; \ k_2=1 \\ \\ t_1=-3-k_1=-3+4=1 \\ t_2=-3-k_2=-3-1=-4$

Обратная замена:

$\left\{\begin{matrix} \frac{x}{y}=t \\ x+y=k\end{matrix}\right. \\ \\ 1) \ \left\{\begin{matrix} \frac{x}{y}=1 \\ x+y=-4\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x=y \\ y+y=-4\end{matrix}\right. \Leftrightarrow \ \left\{\begin{matrix} x=y \\ 2y=-4\end{matrix}\right. \Leftrightarrow \ \left\{\begin{matrix} x=-2 \\ y=-2\end{matrix}\right.$

$2) \ \ \left\{\begin{matrix} \frac{x}{y}=-4 \\ x+y=1\end{matrix}\right. \Leftrightarrow \left\{\begin{matrix} x=-4y \\ -4y+y=1\end{matrix}\right. \Leftrightarrow \ \left\{\begin{matrix} x=-4y \\ -3y=1\end{matrix}\right. \Leftrightarrow \ \left\{\begin{matrix} x=\frac{4}{3} \\ y=-\frac{1}{3} \end{matrix}\right.$

Приложения:

ozokjl: первое уравнение расплющило сильно, можете пожалуйста написать здесь?

life092: Здравствуйте помогите пожалуйста задание в профиле опубликовала по алгебре помогите пожалуйста

Похожие вопросы

Русский язык

1 год назад

5 словосоченений -н- срроооооочччннннооооо плииииииз!!!!!!!!!!!!!

Русский язык

1 год назад

Морфологический разбор слова не утоптанному

Английский язык

2 года назад

помгите с тестом Test “Present Perfect Progressive”. 1) Use Present Perfect Progressive. 1. I’m tired. I (work) all day. 2. She (study) English for five years. 3. I (travel) a lot since you

Математика

2 года назад

Вычислите удобным способом -32,3 ∙ 4+ 6 ∙(-32,3)

Математика

8 лет назад

План местности разбит на клетки

Геометрия

8 лет назад

найдите угол BAC если градусная мера дуги АС =80

Математика

9 лет назад

На покупку тетрадей Сережа затратил 60 р,а Коля на 3/4 этой суммы больше. Сколько денег потратил Коля?

Биология

9 лет назад

может ли одна клетка быть самостоятельным организмом?Как вы объясните это?