Предмет: Алгебра
Автор: Ифигения
Вопрос задан 7 лет назад

< >

Найти дифференциал функции
y = arctg sinx/x

Приложения:

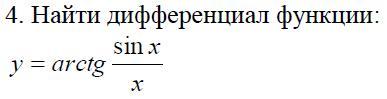
VlaDikantro: Тебе с полным решением илм только ответ?

Ифигения: Конечно полное)

VlaDikantro: Ок

Ответы

Ответ дал: NNNLLL54

4

Ответ:

$\displaystyle y=arctg\dfrac{sinx}{x}\\\\\\y'=\frac{1}{1+\dfrac{sin^2x}{x^2}}\cdot \frac{sinx-x\cdot cosx}{sin^2x}=\frac{x^2}{x^2+sin^2x}\cdot \frac{sinx-x\cdot cosx}{sin^2x}\\\\\\dy=\frac{x^2}{x^2+sin^2x}\cdot \frac{sinx-x\cdot cosx}{sin^2x}\cdot dx$

Ифигения: <3 <3 <3

Похожие вопросы

Другие предметы

1 год назад

Пожалуйста подскажите как нарисовать менятею по Изо срочно

Английский язык

1 год назад

Ted is tired and needs a day off.What does he say?

Английский язык

2 года назад

Forest and jungle animals are in ________________ because we are cutting down trees.

История

2 года назад

правознавство!!!дуже потрібно допоможіть будь ласка !!!

Литература

8 лет назад

Синквейн волк на псарне

Литература

8 лет назад

помогите умоляю . помогите составить вопросы к произведению льва Толстого два брата . думаю вы знаете этот текст

Математика

9 лет назад

Перевести число 75 из десетичной системы в двоичную,восьмеричную и шестнадцатеричную систему счисления

Математика

9 лет назад

Помогите пожалуйста выполнить номер 1348. Ответ полный с решением , заранее спасибо ! За проделанную работу достойная награда!