Вынести множитель за знак корня.

Желательно с обьяснением или пошаговое решение.

Ответ:

Пошаговое объяснение:

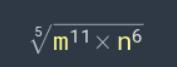
1. Представим показатель степени в виде суммы, в которой одно слагаемое кратно показателю корня:

2. Используя формулу:

, запишем выражение в развёрнуто виде:

3. Любое выражение в степени 1 равно самому себе:

4. Корень из произведения равен произведению корней из каждого множителя:

5. Сократить степени корня и показателя степени на 5:

Да пожаааалуйста корону.

Ответ:

Пошаговое объяснение:

представим подкоренное выражение в виде произведения, используя свойство степени