Предмет: Геометрия
Автор: kepaaaclown
Вопрос задан 7 лет назад

< >

Знайдіть косинуси кутів трикутника зі сторонами: 5 см, 6 см і 7 см.

Ответы

Ответ дал: mathkot

6

Ответ:

$\boxed{ \cos \angle ABC = 0,2 }$

$\boxed{ \cos \angle BCA = \dfrac{5}{7} }$

$\boxed{ \cos \angle CAB = \dfrac{19}{35} }$

Объяснение:

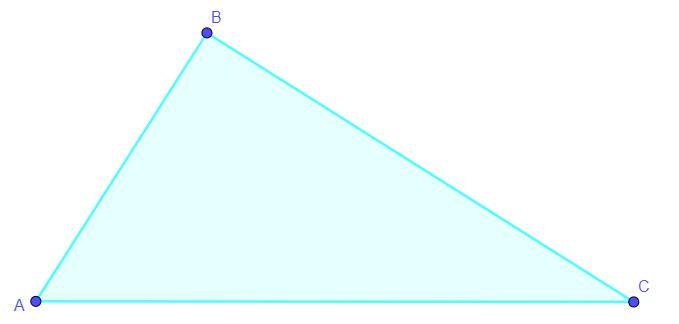
Дано: AB = 5 см, BC = 6 см, AC = 7 см

Знайти: cos ∠ABC, cos ∠BCA, ∠CAB - ?

Розв'язання: За теоремою косинусів для трикутника ΔABC:

$AB^{2} + BC^{2} - 2 \cdot AB \cdot BC \cdot \cos \angle ABC = AC^{2} \Longrightarrow$

$\cos \angle ABC =\dfrac{AB^{2} + BC^{2} - AC^{2}}{2 \cdot AB \cdot BC} =\dfrac{5^{2} + 6^{2} - 7^{2}}{2 \cdot 5 \cdot 6} = \dfrac{25 + 36 - 49}{60} = \dfrac{12}{60} = 0,2$

$AB^{2} + AC^{2} - 2 \cdot AB \cdot AC \cdot \cos \angle CAB = BC^{2} \Longrightarrow$

$\cos \angle CAB = \dfrac{AB^{2} + AC^{2} - BC^{2}}{2 \cdot AB \cdot BC} = \dfrac{5^{2} + 7^{2} - 6^{2}}{2 \cdot 5 \cdot 7} = \dfrac{25 + 49 - 36}{70} = \dfrac{38}{70} = \dfrac{19}{35}$

$BC^{2} + AC^{2} - 2 \cdot BC \cdot AC \cdot \cos \angle BCA = AB^{2} \Longrightarrow$

$\cos \angle BCA = \dfrac{BC^{2} + AC^{2} - AB^{2}}{2 \cdot BC \cdot AC} = \dfrac{6^{2} + 7^{2} - 5^{2}}{2 \cdot 6 \cdot 7} = \dfrac{36 + 49 - 25}{84} = \dfrac{60}{84} = \dfrac{5}{7}$

Приложения:

Похожие вопросы

Окружающий мир

1 год назад

Описать клевер: Как выглядят его корни Сколько стеблей у него Какие они( то есть стебли) Какие листья Как они прикрепляются к стеблю Как выглядят цветки у клевера Есть ли плоды? Если есть, какие

Английский язык

1 год назад

Выберите правильный ответ

Алгебра

2 года назад

При каких значениях х функция у=6-х/5 -2

Физика

2 года назад

нікелювання металевої пластини площею 30 см квадратних тривало протягом 500 секунд за сили струму 0 ,9 А . Знайдіть товщину шару нікелю на пластині. Електрохімічний елемент нікелю 3 * 10 мінус 7

Литература

8 лет назад

СКАЗКА О ПОТЕРЯННОМ ВРЕМЕНИ-о чем говориться в сказке?пожалуйста помоги

Информатика

8 лет назад

Используя Рекурсивную функцию вычислить 3^(9) три девятой степени только с полным кодом.

Математика

9 лет назад

652-x=14+38 реши уравнения

Математика

9 лет назад

(37,8-19,1)*4=? P.S. Примеры по столбикам