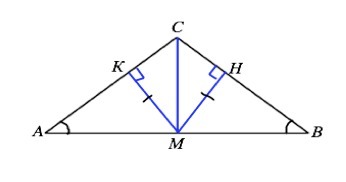
На основании АВ равнобедренного треугольника АВС взята точка М, равноудаленная от боковых сторон.Докажите, что СМ - высота треугольника АВС.
Ответы
Точка М равноудалена от АС и ВС, т.е. находится на равном от этих сторон расстоянии.
Расстояние от точки до прямой измеряется длиной орезка, проведенного перпендикулярно.
МК⊥АС, МН⊥ВС и КМ=МН
В прямоугольных ∆ АКМ и ∆ ВНМ равны острые углы А = В ( углы при основании равнобедренного треугольника), значит, равна и другая пара острых углов: ∠КМА=∠НМВ.
Катет КМ=катету МН ( по условию)
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.=>
∆ АКМ =∆ ВНМ , следовательно, АМ=ВМ.
∆ АМС = ∆ ВМС по двум сторонам и углу между ними. =>
∠СМА=∠СМВ, они смежные и равны 180°:2=90° .⇒
СМ - проведена из вершины угла треугольника к противоположной стороне, перпендикулярна ей, следовательно, СМ - высота треугольника АВС