ДАЮ ДОФИГА БАЛЛОВ !
ВСЁ УКАЗАНО НА КАРТИНКЕ!
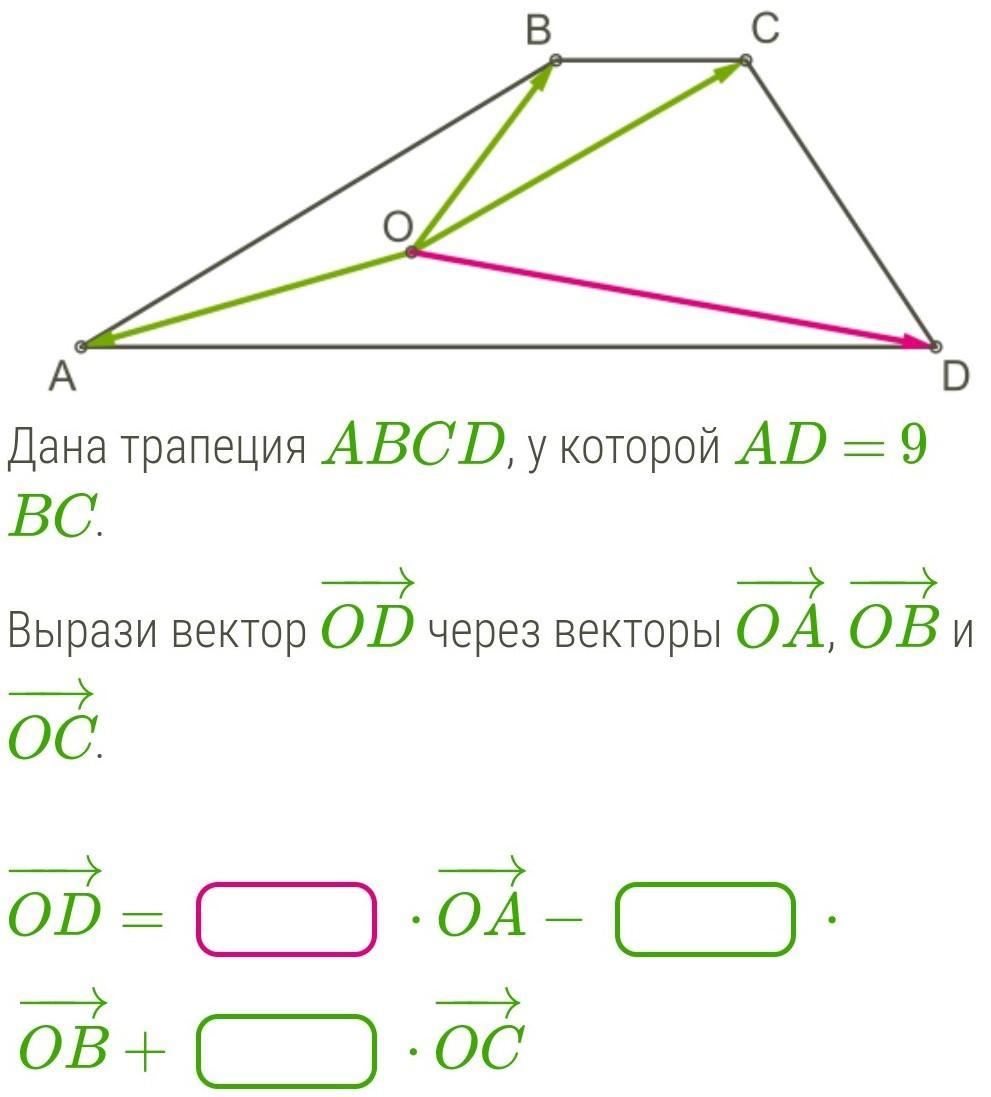
Дана трапеция ABCD, у которой AD = 9BC.
Вырази вектор OD−→− через векторы OA−→−, OB−→− и OC−→−.

OD−→−=
⋅OA−→−−
⋅OB−→−+
⋅OC−→−​

Ответ:

Объяснение:

Определим вектор ОD через те векторы, которые можно построить на рис.:

Векторы и коллинеарны и однонаправлены.

Вектор

Т.к. вектор ВО - это тот же вектор ОВ, но направленный в противоположную сторону,

то

Т.к. AD = 9BC, очевидно, что

Отсюда: