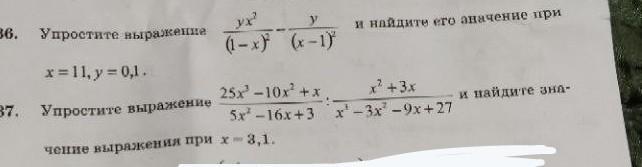Предмет: Алгебра
Автор: voutvovovolalvarvour
Вопрос задан 7 лет назад

< >

Ответье пожалуйста..

Приложения:

Ответы

Ответ дал: Avantgardе

1

Поскольку при возведении в квадрат любого числа получаем положительный ответ, то не имеет значения, в каком порядке располагаются числа в знаменателе, то есть

$(x-1)^2=(1-x)^2$

$\dfrac{yx^2}{(1-x^2)}-\dfrac{y}{(x-1)^2}=\dfrac{yx^2-y}{(x-1)^2}=\dfrac{y(x^2-1)}{(x-1)^2}=\dfrac{y(x-1)(x+1)}{(x-1)^2}=\dfrac{y(x+1)}{x-1}$

При x = 11 ; y = 0,1

$\dfrac{0.1(11+1)}{11-1}=\dfrac{0.1\cdot12}{10}=\dfrac{1.2}{10}=0.12$

Ответ: 0,12

$\dfrac{25x^3-10x^2+x}{5x^2-16x+3}:\dfrac{x^2+3x}{x^3-3x^2-9x+27}=$

$=\dfrac{x(25x^2-10x+1)^2}{5x^2-x-15x+3}\cdot\dfrac{x^3+27-3x^2-9x}{x(x+3)}=$

$=\dfrac{(5x-1)^2}{x(5x-1)-3(5x-1)}\cdot\dfrac{(x+3)(x^2-3x+9)-3x(x+3)}{x+3}=$

$=\dfrac{(5x-1)^2}{(5x-1)(x-3)}\cdot\dfrac{(x^2-3x+9-3x)(x+3)}{x+3}=$

$=\dfrac{5x-1}{x-3}\cdot\dfrac{(x-3)^2}{1}=(5x-1)(x-3)=5x^2-15x-x+3=5x^2-16x+3$

При x = 3,1

$5\cdot3.1^2-16\cdot3.1+3=48.05-49.6+3=3-1.55=1.45$

Ответ: 1,45

Похожие вопросы

Английский язык

1 год назад

Помогите, пожалуйста, перевести на английский 5. Мой брат прекрасно владеет немецким языком. Он окончил немецкое отделение университета два года тому назад. 6. Когда вы будете готовиться к

Қазақ тiлi

1 год назад

Помогите пожалуйста просклонять по падежам на казахском языке екі дәптер

Биология

2 года назад

Ролью лишайников в природе не является: 1) Образуют почву. 2) Разлагают отмершие остатки. 3) Являются кормом для некоторых животных.

Алгебра

2 года назад

помогите пожалуйста 1час мучаюсь не могу сделать задание

Математика

8 лет назад

12т 15 кг - 98 кг =?(переведите в тонны и килограммы

Геометрия

8 лет назад

Боковое ребро прямой призмы равно 10 см , а ее объем - 200 см3 . Основание призмы - равнобокая трапеция с основаниями 2 и 8 см . Найдите полную поверхность призмы

Математика

9 лет назад

найди правило по которому записаны тройки виличин и впиши пропушиные числа 220см 2м 2дм __см 5дм 80мм. __мин 1ч 10 мин __см 6м 6дм __мм 5дм 5 см. Срочно надо

Литература

9 лет назад

стихотворения Некрасова не менее 30 строк