знайдіть висоту правильної трикутної піраміди, сторона основи якої дорівнює b, а бічна грань утворює з площиною кут a

Ответ:

Пошаговое объяснение:

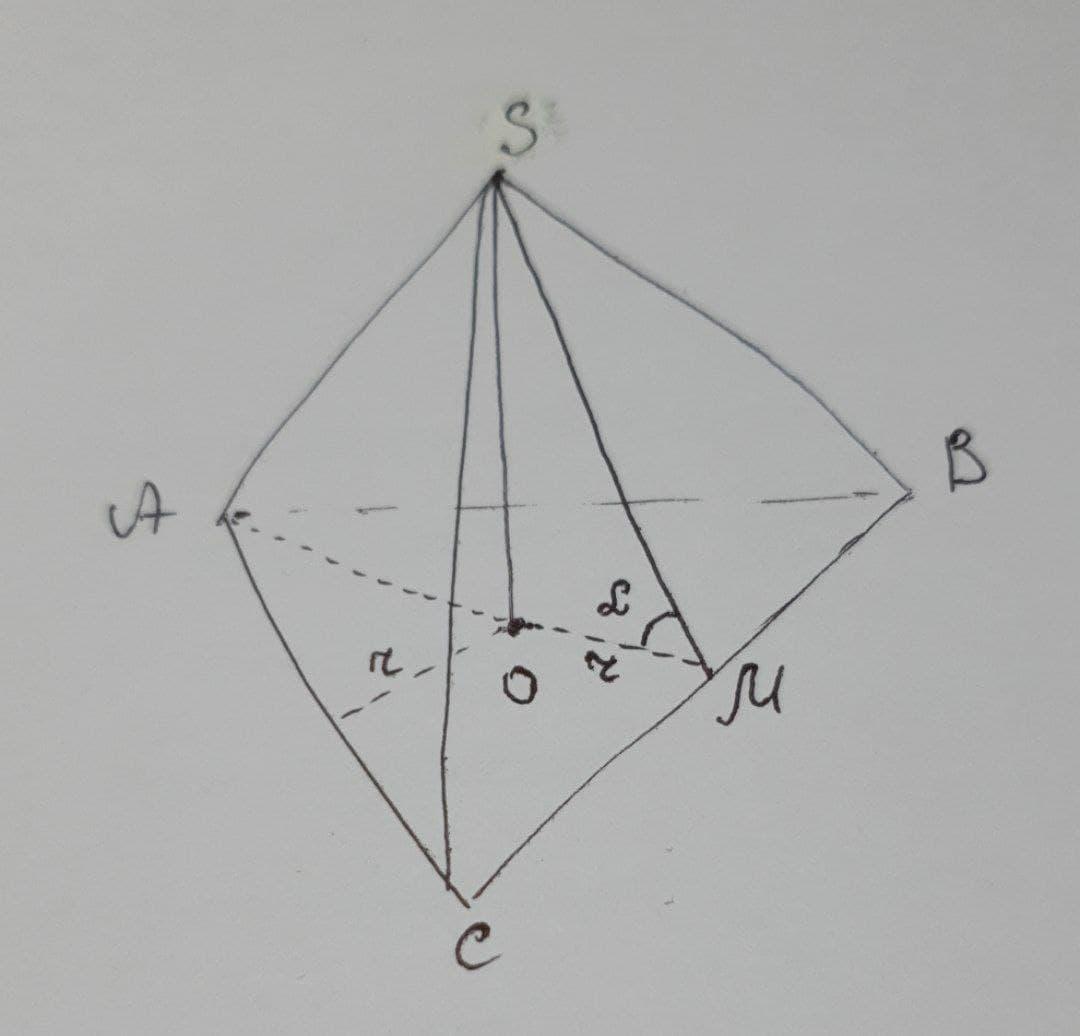
Маємо правильну трикутну піраміду SABC, в основі якої лежить правильний (рівносторонній) трикутник ABC. Нехай довжина його сторони рівна в.

Висота SO правильної трикутної піраміди проектується у центр вписаного в трикутник ABC  кола.

Радіус вписаного кола:  r = MO = b/ 2√3

За властивістю радіуса вписаного кола: MO⊥BC.

Оскільки висота SO перпендикулярна до площини основи (трикутника ABC), то вона перпендикулярна до кожної прямої, що лежить в цій площині, тому SO⊥OM.

Відрізок SM – похила, а OM – проекція похилої на площину основи (ΔABC), тому ∠SMO=α – кут нахилу бічной грані до площини основи.

З прямокутного ΔSOM(∠O = 90°) : h = SO = MO*tg α = b/ 2√3 * tg α