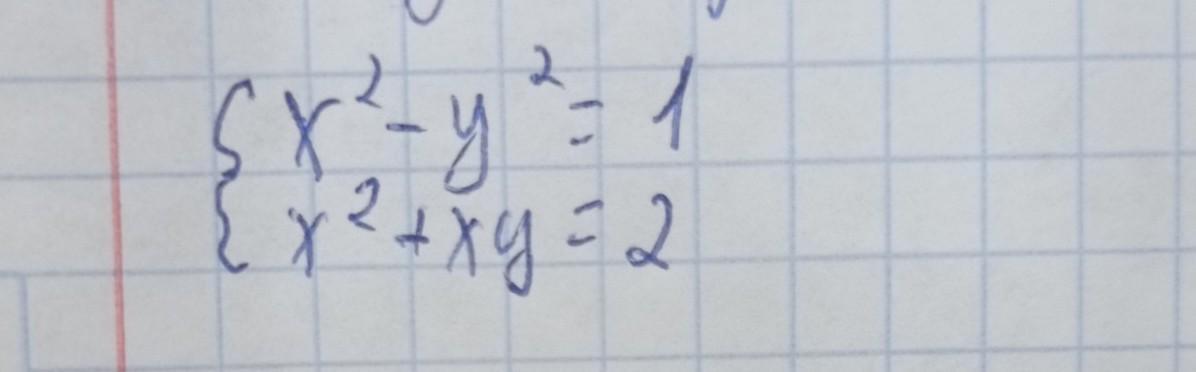Предмет: Алгебра
Автор: markoy19
Вопрос задан 7 лет назад

< >

решите систему уравнений

Приложения:

Ответы

Ответ дал: sangers1959

0

Объяснение:

$\left \{ {{x^2-y^2=1} \atop {x^2+xy=2}} \right. \ \ \ \ \ \left \{ {{(x+y)*(x-y)=1} \atop {x*(x+y)=2}} \right. \ \ \ \ \ \left \{ {{\frac{2}{x} *(x-y)=1} \atop {x+y=\frac{2}{x} }} \right.\ \ \ \ \left \{ {{x-y=\frac{x}{2} } \atop {x+y=\frac{2}{x} }} \right. .$

Суммируем эти уравнения:

$2x=\frac{x}{2}+\frac{2}{x} \ |*2x\ \ \ \ \ x\neq 0\\4x^2=x^2+4\\3x^2=4\ |:4\\x^2=\frac{4}{3} \\x_{1,2}=б\sqrt{\frac{4}{3} } =б\frac{2}{\sqrt{3} } =б\frac{2\sqrt{3} }{3} .\\x_1=\frac{2\sqrt{3} }{3}.\\ (\frac{2\sqrt{3} }{3})^2+\frac{2\sqrt{3} }{3}*y=2\\\frac{4}{3} +\frac{2\sqrt{3} }{3}*y =2\\\frac{2\sqrt{3} }{3}*y =\frac{2}{3} \ |*\frac{3}{2}\\\sqrt{3} *y=1 \ |:\sqrt{3} \\y_1=\frac{1}{\sqrt{3} }=\frac{\sqrt{3} }{3}. \\x_2=-\frac{2\sqrt{3} }{3}.\\$

$(-\frac{2\sqrt{3} }{3})^2+(-\frac{2\sqrt{3} }{3})*y=2\\\frac{4}{3} -\frac{2\sqrt{3} }{3}*y =2\\\frac{2\sqrt{3} }{3}*y =-\frac{2}{3} \ |*\frac{3}{2}\\\sqrt{3} *y=-1 \ |:\sqrt{3} \\y_2=-\frac{1}{\sqrt{3} }=-\frac{\sqrt{3} }{3}. \\$

Ответ: (2√3/3;√3/3) (-2√3/3;-√3/3).

Похожие вопросы

Русский язык

1 год назад

Ребята прошу помочь мне нужно сочинение на тему ИНСТРУКЦИЯ ПО ИСПОЛЬЗОВАНИЮ ВОЛШЕБНОЙ ПАЛОЧКИ

Русский язык

1 год назад

Подчеркните главные члены и укажите части речи.стоит чудесный зимний день

Математика

2 года назад

всі бічні грані правильної трикутної піраміди нахилені до площини основи під кутом 60, а висота піраміди 9. знайдіть об'єм піраміди

Алгебра

2 года назад

Пожалуйста помогите. Дам 10 баллов!

Математика

8 лет назад

заполни таблицу. Длина прямоугольника 8мм 10см ,ширина прямоугольника 4 мм, ?, периметр прямоугольника ? 32 см.

Физика

8 лет назад

Рома и Витя умеют поднимать грузы массой 60 кг каждый. Однажды, они несли бревно длиной 3 м и массой 120 кг, схватившись по краям. Вдруг, из-за несогласованности действий, один из концов бревна

Химия

9 лет назад

ПОМОГИТЕ ВЫБРАТЬ ПРАВИЛЬНЫЙ ОТВЕТ! Бромоводородная кислота реагирует с: 1) карбонатом кальция 2) оксидом кремния 3) оксидом хрома(|||) 4) нитратом свинца(||) 5)алюминием 6) сульфатом меди(||)

Литература

9 лет назад

И становится ясно, кто врал и работал по принципу «У-2»: угадать и угодить. Когда … Дополните фразу