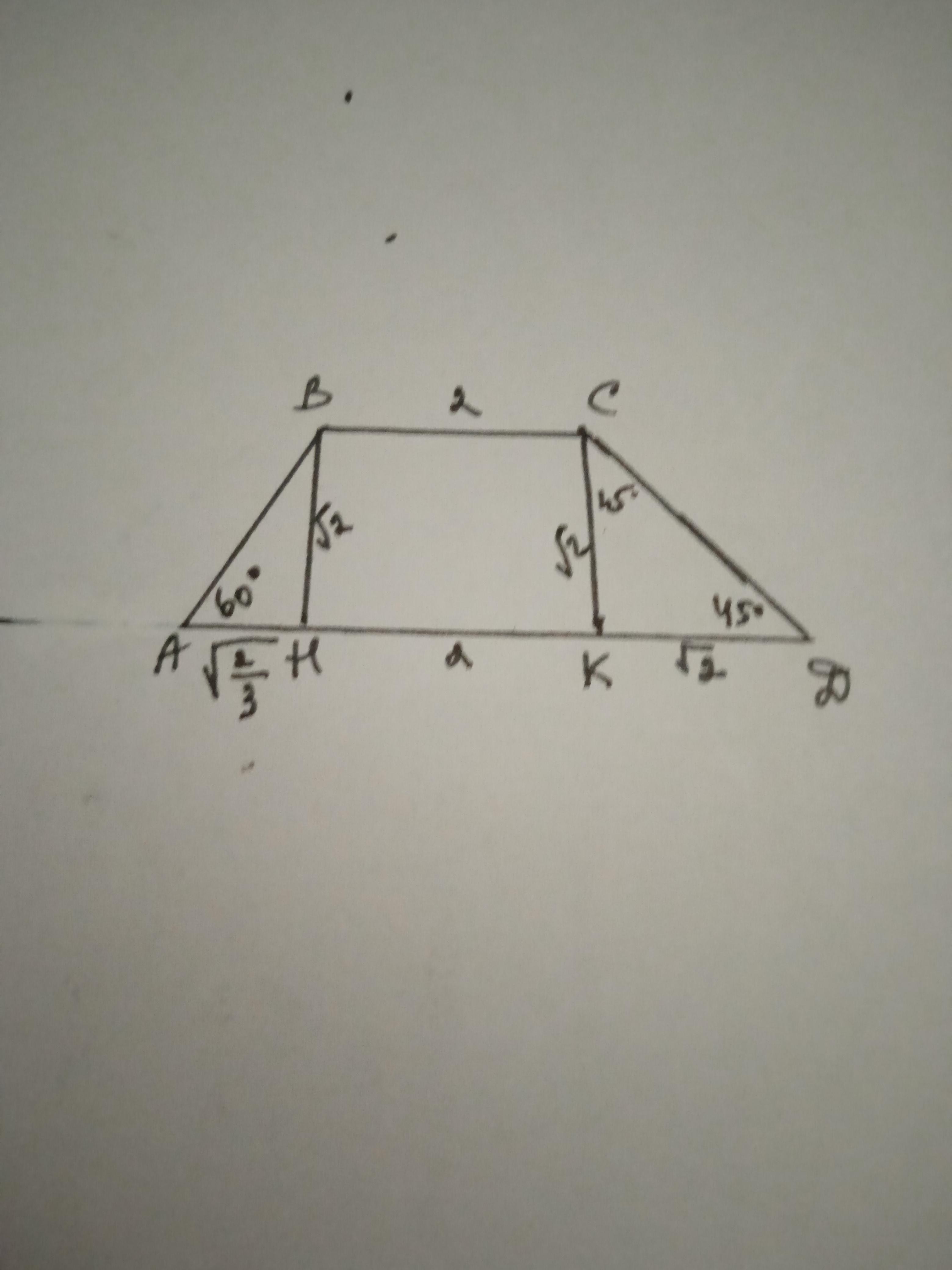
2. в трапеции abcd BC||AD угол a = 60°, угол d = 45°, вс = 2, высота трапеции √2. найдите периметр трапеции.​

Ответ:

8 4/9 + √2 + √(2/3) ≈ 10,72 ед.

Объяснение:

∠АВН=90-60=30°

По теореме синусов АН=1/2 * √2 : √3/2 = √(2/3).

По теореме Пифагора АВ=(ВН²+АН²)=(√2)² + √(2/3)²=2 +  4/9 = 2 4/9.

ΔСКD - равнобедренный, т.к. ∠СКD=90-45=45°;  КD=СК=√2.

По теореме Пифагора СD = (√2)² + (√2)² = √4 = 2.

Р=2 4/9 + 2 + 2 + √2 + 2 + √(2/3) = 8 4/9 + √2 + √(2/3) ≈ 10,72 ед.