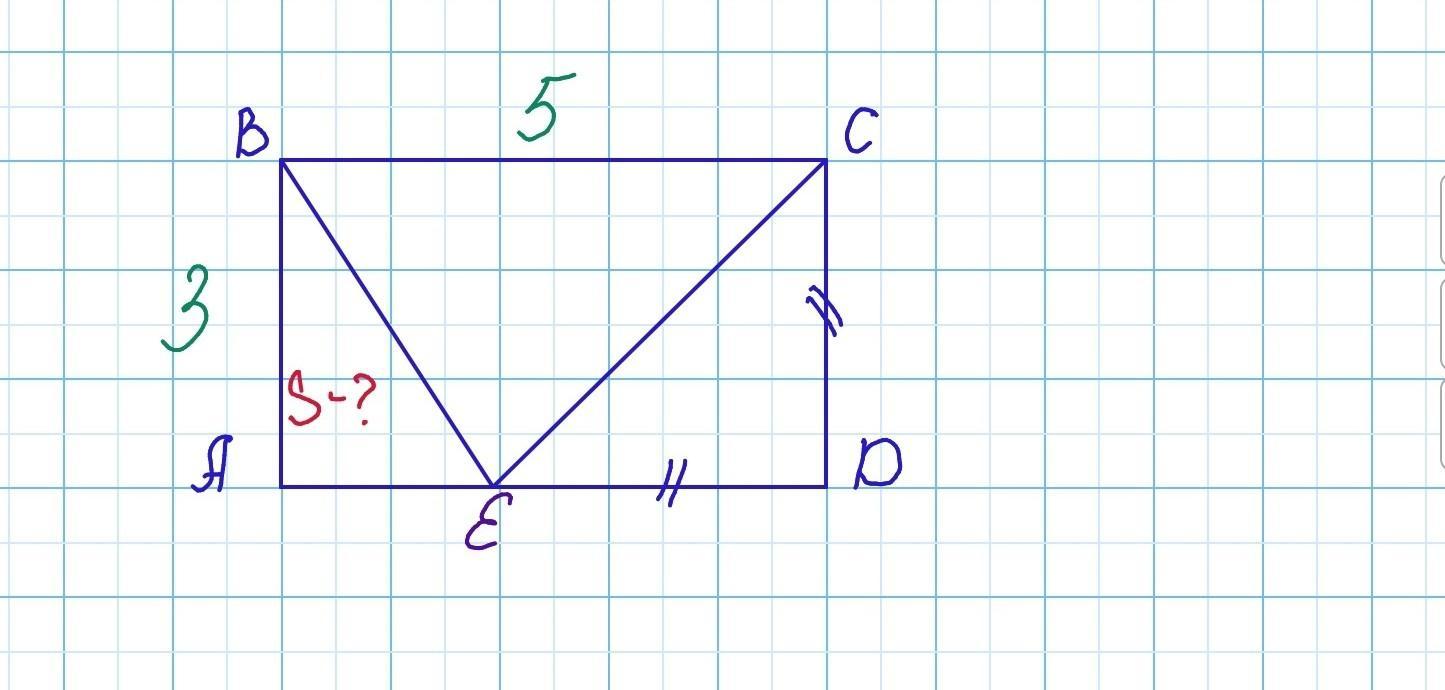
В прямоугольнике ABCD AB = 3, BC = 5. на стороне AD отмечена точка E такая, что треугольник CDE - равнобедренный. Найдите площадь треугольника ABE.

Ответ:

3 ед²

Объяснение:

В прямоугольнике противоположные стороны равны, поэтому CD=AB=3 ед, AD=BC=5 ед.

△CDE - равнобедренный. В равнобедренном треугольнике боковые стороны равны: ED=CD=3 ед.

AE=AD-ED=5-3=2 ед.

△ABE -прямоугольный (∠С=90°).

Площадь прямоугольного треугольника равна половине произведения его катетов.

ед²