1)сократите дробь 4-х²/7х²-9х-10

2)решите уравнение х+2/х=5х+1/х+1

ПОМОГИТЕ ПОЖАЛУЙСТА, ДАЮ 30 БАЛЛОВ

Приложения:

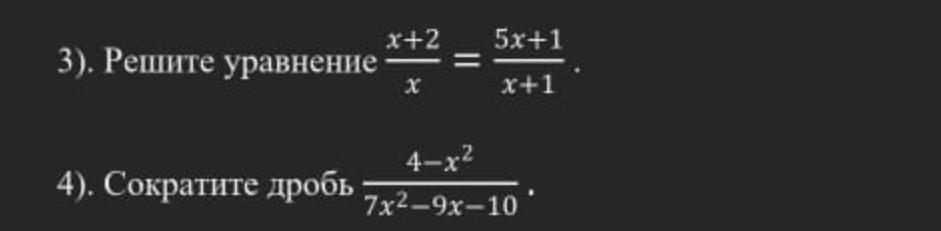
Ответы

Ответ дал: Dmitry1986

Вложение фото решения, ответа.

Приложения:

pufikovpufik: спасибо большое

Ответ дал: elenamuraweva

Ответ:

$\frac{x + 2}{x} = \frac{5x + 1}{x + 1} \\ \frac{(x + 2)(x + 1)}{x(x + 1)} = \frac{(5x + 1)x}{x(x + 1)} \\ {x}^{2} + x + 2x + 2 = 5 {x}^{2} + x \\ {x}^{2} + 3x + 2 - 5 {x}^{2} - x = 0 \\ - 4 {x}^{2} + 2x + 2 = 0 | \div ( - 4) \\ {x}^{2} - \frac{1}{2} x - \frac{1}{2} = 0 \\ d = {b}^{2} - 4ac = {( - \frac{1}{2}) }^{2} - 4 \times 1 \times ( - \frac{1}{2} ) = \frac{1}{4} + 2 = 2 \frac{1}{4} = \frac{9}{4} \\ x1 = \frac{ - b - \sqrt{d} }{2a} = \frac{ - ( - \frac{1}{2}) - \sqrt{ \frac{9}{4} } }{2 \times 1} = \frac{ \frac{1}{2} - \frac{3}{2} }{2} = - \frac{1}{2} \\ x2 = \frac{ - b + \sqrt{d} }{2a} = \frac{ - ( - \frac{1}{2}) + \sqrt{ \frac{9}{4} } }{2 \times 1} = \frac{ \frac{1}{2} + \frac{3}{2} }{2} = \frac{2}{2} = 1$

$\frac{4 - {x}^{2} }{7 {x}^{2} - 9x - 10 } \\$

Найдем корни знаменателя

$7 {x}^{2} - 9x - 10 = 0 \\ d = {b}^{2} - 4ac = {( - 9)}^{2} - 4 \times 7 \times ( - 10) = 81 + 280 = 361 \\ x1 = \frac{ - b - \sqrt{d} }{2a} = \frac{ - ( - 9) - \sqrt{361} }{2 \times 7} = \frac{9 - 19}{14} = \frac{ - 10}{14} = - \frac{5}{7} \\ x2 = \frac{ - b + \sqrt{d} }{2a} = \frac{ - ( - 9) + \sqrt{361} }{2 \times 7} = \frac{9 + 19}{14} = \frac{ 28}{14} = 2$

Значит корни уравнения

$x1 = - \frac{5}{7} \\ x2 = 2$

$\frac{4 - {x}^{2} }{7 {x}^{2} - 9x - 10 } = \frac{(2 - x)(2 + x)}{7(x + \frac{5}{7})(x - 2 )} = \\ \frac{ - ( x- 2)(x + 2)}{7(x + \frac{5}{7} )(x - 2)} = - \frac{x + 2}{7x + 5}$