Дано куба ABCD A1 B1 C1 D1 знайти площу перерізу куба площиною яка проходить через вершини B1 і C1 та середину ребра DD1 якщо ребро куба дорівнює
Приложения:
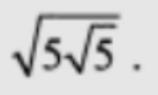
Ответы
Ответ дал:
1
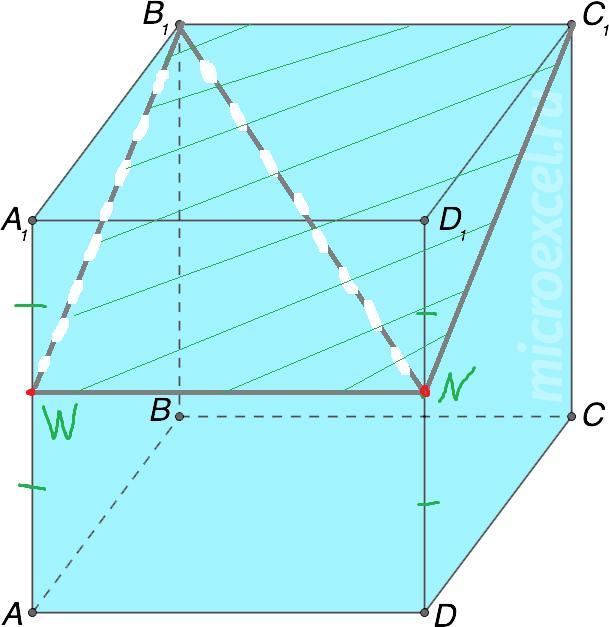
Пусть N - середина ребра DD₁. Через точку W - середину ребра АА₁ проведём отрезок В₁W║NC₁, тогда прямоугольник В₁С₁NW и будет искомым сечением, чью площадь обозначим за S, а ребро куба за b.
Дано: b = D₁C₁ = , ND₁ = 0,5·D₁C₁ =
. Далее в ΔD₁NC₁ по теореме Пифагора: NC₁² = D₁C₁² + ND₁² = b² + (0,5b)² = b² +
⇒ NC₁ =
⇒
площадь сечения равна:
S = В₁C₁ · NC₁ =
Ответ: площадь сечения равна 12,5
Приложения:
Похожие вопросы
2 года назад
2 года назад
8 лет назад
9 лет назад