Предмет: Геометрия
Автор: Аноним
Вопрос задан 10 лет назад

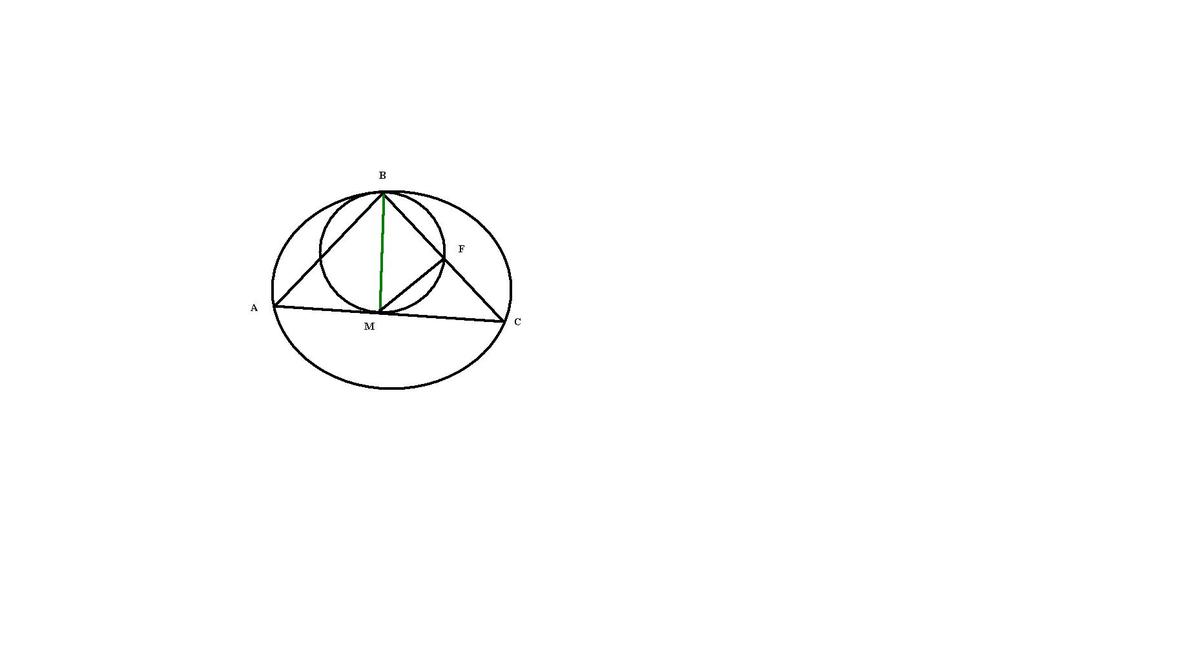
Медиана BM треугольника ABC является диаметром
окружности, пересекающей сторону BC в её середине. Найдите этот диаметр,
если диаметр описанной окружности треугольника ABC равен 8 .

Ответы

Ответ дал: Матов

Если $BM$ медиана то $AM=MC$ , по условию следует что $BF=FC$ . Если мы проведем отрезок $MF$ то получим прямоугольные треугольники $BFM MFC$ .
Заметим что треугольник $BMC$ равнобедренный так как $MF$ высота делящая сторону $BC$ пополам - это свойственно равнобедренному либо равностороннем треугольникам . Треугольник $ABM$ так же равнобедренный поскольку $BM=BM=AM$ . Если теперь обозначить угол $BAC=a$ то в треугольнике $ABC$ $4a=180\ a=45а$ то есть треугольник $ABC$ - прямоугольный , следовательно $AC=8$ откудо $BM=4$
Ответ $4$