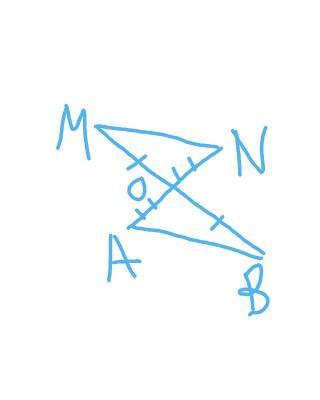
4. Отрезки MB=24 см и АN=18 см пересекаются в точке
ОиВ этой точке делятся пополам. Найдите длину отрезка
AB, если периметр треугольника MNO равен 29 см.

Треугольники АОВ И NOM равны по первому признаку равенства треугольников, в них стороны AO=NO=18/2=9

MO=BO=24/2=12

∠NOM=∠AOB как вертикальные, значит, из равенства треугольников вытекает равенство сторон АВ=MN=29-9-12=8

Ответ 8

Пошаговое объяснение:

Рассмотрим тр-к МNO и тр-к АВО:

МО=ВО - по условию

АО=NO - по условию

<MON=<BOA - как вертикальные

Тр-ки равны по 2 сторонам и углу между ними ( по 1 признаку), значит соответствующие элементы равны.

Р(МNO) =MN+NO+MO

MO=MB:2=24:2=12 cм

NO=AN:2=18:2=9 cм

29=МN+9+12

29=MN+21

MN=29-21

MN=8 cм

АВ=MN=8 cм