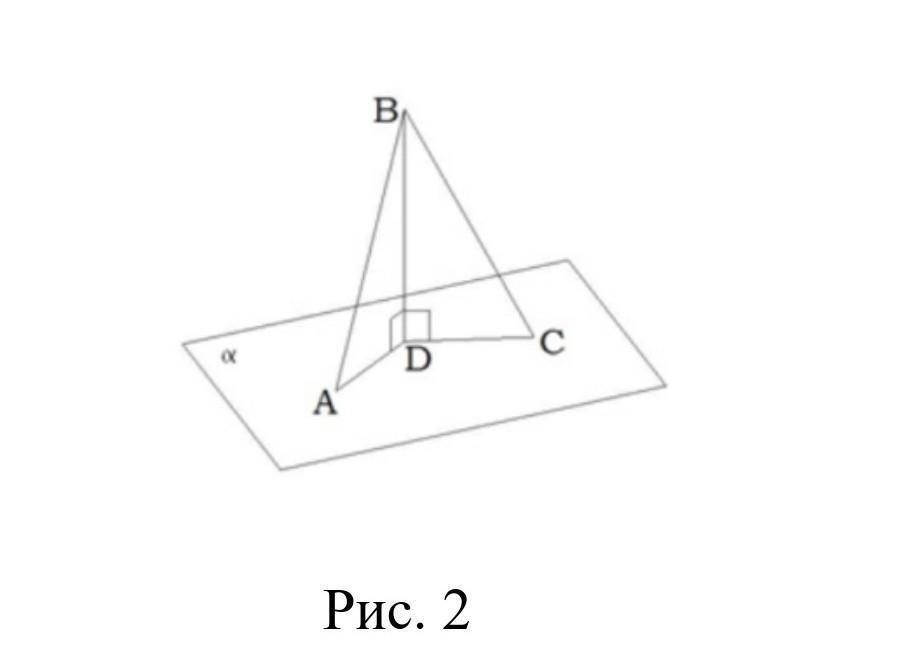
К плоскости проведен перпендикуляр BD и наклонные ВА и ВС (рис. 2). Известно, что ВА = 6 см, ∟АВD = 30 градусов, ∟СВD = 45 градусов. Найдите длины проекций наклонных ВА и ВС. ​

Ответ:

АD=3см

DC=3√3см

Объяснение:

∆АВD- прямоугольный треугольник

АD- катет против угла <АВD=30°

AD=AB/2=6/2=3см

По теореме Пифагора

ВD=√(AB²-AD²)=√(6²-3²)=√(36-9)=

=√27=3√3 см.

∆СВD- прямоугольный треугольник

Углы: <ВDC=90°,по условию; <СВD=45°, по условию; <ВСD=180°-90°-45°=45°.

Углы при основании равны, ∆СВD- равнобедренный треугольник. ВD=DC=3√3см