Алгебра. Даю 30 баллов.
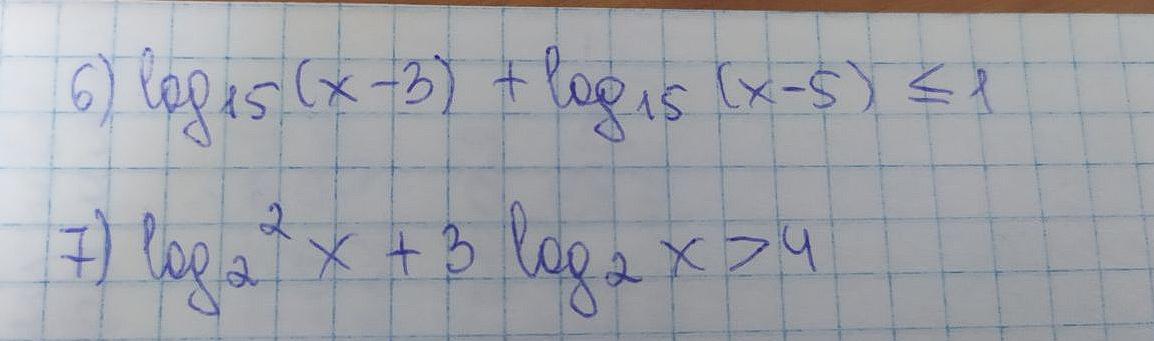
Ответы
Ответ:
6)
7) x ∈ (0, 1/16) ∪ (2, +∞)
Объяснение:
6) Находим ОДЗ:
,
Откуда
Сумма двух логарифмов по одному основанию есть логарифм произведения подлогарифмических выражений по этому основанию.
㏒15((x-3) * (x-5))
Представим 1 в виде логарифма по основанию 15. Подлогарифмические выражения перемножим.
㏒15(x^2 - 8x + 15) ㏒15(15)
Т.к логарифм - возрастающая функция, то следовательно для решения данного неравенства имеем право убрать логарифмы.
Решаем методом интервалов. Получаем:
Пересекаем с ОДЗ, . Тогда окончательный ответ:
7) Сначала запишем ОДЗ: x > 0.
Решаем методом замены:
t = ㏒2(x)
Тогда
Решаем методом интервалов, корни легко угадываются по Т. Виета, это -4 и 1.
Подставляем вместо t ㏒2x, решаем получившиеся неравенства.
(1) ㏒2x < -4
㏒2x < ㏒2(1/16)
x < 1/16
(2) ㏒2x > 1
㏒2x > ㏒2(2)
x > 2
В (1) помним о том, что по ОДЗ x > 0, перескаем (1) с ОДЗ, добавляем к решению (2) и получаем ответ: